题目内容
(本小题满分12分)
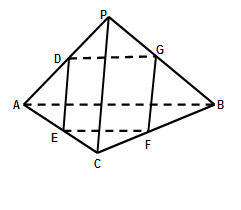
在如图的多面体中,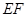 ⊥平面
⊥平面 ,
,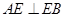 ,
,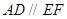 ,
,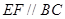 ,
,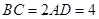 ,
,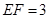 ,
,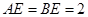 ,
,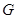 是
是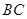 的中点.
的中点.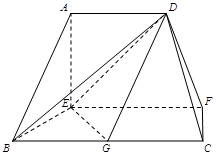
(Ⅰ) 求证: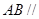 平面
平面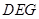 ;
;
(Ⅱ) 求二面角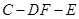 的余弦值.
的余弦值.
(Ⅰ)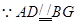 ∴四边形
∴四边形 是平行四边形∴
是平行四边形∴  ∴
∴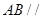 平面
平面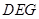 (Ⅱ)
(Ⅱ)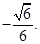
解析试题分析:(Ⅰ)证法一:∵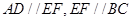 , ∴
, ∴ .
.
又∵ ,
,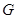 是
是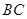 的中点, ∴
的中点, ∴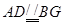 ,
,
∴四边形 是平行四边形, ∴
是平行四边形, ∴  .
.
∵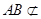 平面
平面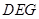 ,
,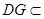 平面
平面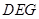 , ∴
, ∴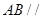 平面
平面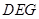 .
.
证法二:∵ 平面
平面 ,
, 平面
平面 ,
,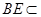 平面
平面 ,
,
∴ ,
, ,又
,又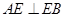 ,∴
,∴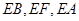 两两垂直.
两两垂直.
以点E为坐标原点,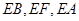 分别为
分别为 轴建立如图的空间
轴建立如图的空间
直角坐标系.
由已知得, (0,0,2),
(0,0,2), (2,0,0),
(2,0,0),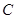 (2,4,0),
(2,4,0),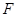 (0,3,0),
(0,3,0), (0,2,2),
(0,2,2),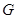 (2,2,0)
(2,2,0) ,
,
设平面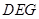 的法向量为
的法向量为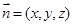
则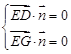 ,即
,即 ,令
,令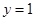 ,得
,得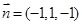 .
.
∴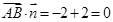 ,即
,即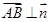 .
.
∵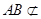 平面
平面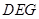 , ∴
, ∴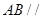 平面
平面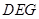 .
.
(Ⅱ)由已知得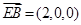 是平面
是平面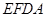 的法向量.
的法向量.
设平面 的法向量为
的法向量为 ,∵
,∵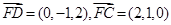 ,
,
∴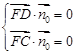 ,即
,即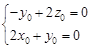 ,令
,令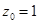 ,得
,得 .
.
则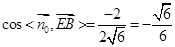 , ∴二面角
, ∴二面角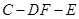 的余弦值为
的余弦值为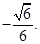
考点:空间线面平行的判定及二面角的求解
点评:利用向量法求解空间几何问题比其他方法思路简单

练习册系列答案
相关题目
 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.
 中.
中.
 与
与 所成的角;
所成的角; ⊥平面
⊥平面 .
.
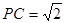 ,求四面体PABC的体积.
,求四面体PABC的体积.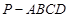 中,底面
中,底面 为矩形,
为矩形,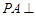 平面
平面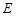 在线段
在线段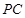 上,
上,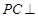 平面
平面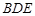 .
.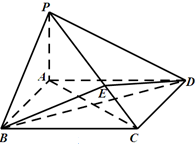
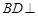 平面
平面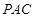 ;
;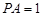 ,
,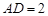 ,求二面角
,求二面角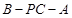 的正切值.
的正切值. 分别是
分别是 中点)
中点)
 平面
平面 ;
; 的体积.
的体积.
 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值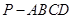 的底面
的底面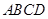 是矩形,
是矩形,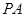 ⊥平面
⊥平面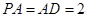 ,
,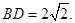
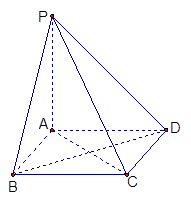
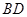 ⊥平面
⊥平面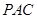 ;
;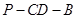 的大小;
的大小;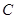 到平面
到平面 的距离.
的距离.