题目内容
函数 定义域为
定义域为 ,若满足①
,若满足① 在
在 内是单调函数;②存在
内是单调函数;②存在 使
使 在
在 上的值域为
上的值域为 ,那么就称
,那么就称 为“成功函数”,若函数
为“成功函数”,若函数 是“成功函数”,则
是“成功函数”,则 的取值范围为( )
的取值范围为( )
A. B.
B. C.
C.  D.
D.

【答案】
C
【解析】依题意,函数 在定义域上为单调递增函数,且t≥0,而t=0时,
在定义域上为单调递增函数,且t≥0,而t=0时, 不满足条件②,∴t>0.设存在[m,n],使得f(x)在[m,n]上的值域为
不满足条件②,∴t>0.设存在[m,n],使得f(x)在[m,n]上的值域为 ,∴
,∴ , 即
, 即
∴m,n是方程 的两个不等实根,∴△=1-4t>0,∴
的两个不等实根,∴△=1-4t>0,∴ .
.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的定义域为
的定义域为 ,若满足:①
,若满足:①
 ,使得
,使得 上的值域为
上的值域为 是定义域为
是定义域为 是定义域为
是定义域为 的“成功函数”,则
的“成功函数”,则 的取值范围为 ( )
的取值范围为 ( ) B.
B.
 C.
C.
 D.
D.

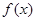 的定义域为D,若满足①
的定义域为D,若满足①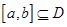 ,使
,使 上的值域为
上的值域为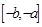 ,那么
,那么 叫做对称函数,现有
叫做对称函数,现有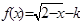 是对称函数, 那么实数k的取值范围是
是对称函数, 那么实数k的取值范围是
 的定义域为
的定义域为 ,若
,若 ,使
,使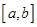 上的值域为
上的值域为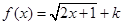 为闭函数,那么
为闭函数,那么 的取值范围是_______。
的取值范围是_______。