题目内容
函数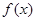 的定义域为D,若满足①
的定义域为D,若满足①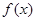 在D内是单调函数,②存在
在D内是单调函数,②存在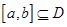 ,使
,使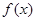 在
在 上的值域为
上的值域为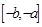 ,那么
,那么 叫做对称函数,现有
叫做对称函数,现有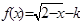 是对称函数, 那么实数k的取值范围是
是对称函数, 那么实数k的取值范围是
【答案】

【解析】 由于 在(-∞,2]上是减函数,故满足①,
在(-∞,2]上是减函数,故满足①,
又f(x)在[a,b]上的值域为[-b,-a],
∴所以 ,
,
即a和 b 是关于x的方程 在(-∞,2]上有两个不同实根.
在(-∞,2]上有两个不同实根.
令t= ,则x=2-t2,t≥0,
,则x=2-t2,t≥0,
∴k=-t2+t+2=-(t- )2+
)2+ ,在[0,+∞]上有两个不同实根,
,在[0,+∞]上有两个不同实根,
又g(t) =-t2+t+2在 递增,在
递增,在 递减且g(0)=2,g(
递减且g(0)=2,g( )=
)=
∴k的取值范围是 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
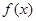 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数 使得对于任意
使得对于任意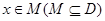 ,有
,有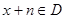 ,且
,且 ,则称
,则称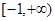 的函数
的函数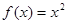 为
为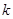 高调函数,那么实数
高调函数,那么实数