题目内容
若n∈N*，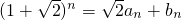
（an，bn∈N*）．
（1）求a4+b4的值；
（2）证明：
；
（3）若[x]表示不超过x的最大整数．试证：当n为偶数时，
．当n为奇数时，上述结果是否依然成立？如果不成立，请用bn表示
（不必证明）
解：（1）(1+√2)4={C}{0{4}}+{C}{1{4}}•√2+{C}{2{4}}(√2)2+{C}{3{4}}(√2)3+{C}{4{4}}(√2)4=12√2+17，所以a4=12，b4=17，a4+b4=29． …（3分）（2）当n为偶数时，(1+√2){n}={C}{0{n}}+{C}{1{n}}•√2+{C}{2{n}}(√2)2+…+{C}{{n}{n}}(√2){n}，b{n}={C}{0{n}}+{C}{2{n}}(√2)2+{C}{4{n}}(√2)4+…+{C}{{n}{n}}(√2){n}，而(1-√2){n}={C}{0{n}}+{C}{1{n}}•(-√2)+{C}{2{n}}(-√2)2+…+{C}{{n}{n}}(-√2){n}，(1+√2){n}+(1-√2){n}=2[{C}{0{n}}+{C}{2{n}}(√2)2+{C}{4{n}}(√2)4+…+{C}{{n}{n}}(√2){n}]，所以b{n}=(1+√2){n}+(1-√2){n}/2成立． …（6分）当n为奇数时，(1+√2){n}={C}{0{n}}+{C}{1{n}}•√2+{C}{2{n}}(√2)2+…+{C}{{n}{n}}(√2){n}，b{n}={C}{0{n}}+{C}{2{n}}(√2)2+{C}{4{n}}(√2)4+…+{C}{{n-1}{n-1}}(√2){n-1}，而(1-√2){n}={C}{0{n}}+{C}{1{n}}•(-√2)+{C}{2{n}}(-√2)2+…+{C}{{n}{n}}(-√2){n}，(1+√2){n}+(1-√2){n}=2[{C}{0{n}}+{C}{2{n}}(√2)2+{C}{4{n}}(√2)4+…+{C}{{n-1}{n-1}}(√2){n-1}]，所以b{n}=(1+√2){n}+(1-√2){n}/2成立． …（9分）（3）由（2）可得2b{n}=(1+√2){n}+(1-√2){n}是正整数，-1＜1-√2＜0，所以当n为偶数时，0＜(1-√2){n}＜1，…（12分）则有2b{n}-1＜(1+√2){n}＜2b{n}，所以2bn-1是不超过(1+√2){n}的最大整数，[(1+√2){n}]=2b{n}-1． …（14分）当n为奇数时，[(1+√2){n}]=2b{n}． …（16分）
练习册系列答案
相关题目