题目内容
(本小题满分14分)
已知函数 为常数,数列
为常数,数列 满足:
满足: ,
, ,
, .
.
(1)当 时,求数列
时,求数列 的通项公式;
的通项公式;
(2)在(1)的条件下,证明对 有:
有: ;
;
(3)若 ,且对
,且对 ,有
,有 ,证明:
,证明: .
.
(1) ,
,
(2)可以用裂项法求和进而证明也可以用数学归纳法证明
(3)可以用基本不等式证明也可以用导数证明,还可以利用数列的单调性证明
解析试题分析:(1)当 时,
时, ,
,
两边取倒数,得 , ……2分
, ……2分
故数列 是以
是以 为首项,为公差的等差数列,
为首项,为公差的等差数列,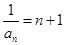 ,
, ,
, . ……4分
. ……4分
(2)证法1:由(1)知 ,故对
,故对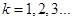

 ……6分
……6分
所以
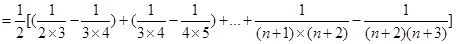

 . ……9分
. ……9分
[证法2:①当n=1时,等式左边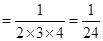 ,等式右边
,等式右边 ,左边=右边,等式成立; ……5分
,左边=右边,等式成立; ……5分
②假设当 时等式成立,
时等式成立,
即 ,
,
则当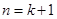 时
时


这就是说当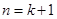 时,等式成立, ……8分
时,等式成立, ……8分
综①②知对于 有:
有: . ……9分】
. ……9分】
(3)当 时,
时,
则 , ……10分
, ……10分
∵ ,
,
∴ ……11分
……11分


 . ……13分
. ……13分
∵ 与
与 不能同时成立,∴上式“=”不成立,
不能同时成立,∴上式“=”不成立,
即对 ,
, . ……14分
. ……14分
【证法二:当 时,
时, ,
,
则 ……10分
……10分
又


已知i为虚数单位,a∈R,若(a-1)(a+1+i)=a2-1+(a-1)i是纯虚数,则a的值为( )
| A.-1或1 | B.1 | C.3 | D.-1 |
复数 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
复数 的共轭复数是( )
的共轭复数是( )
A. | B. | C. | D. |
 是菱形,
是菱形, 是矩形,
是矩形, 平面
平面 ,
, .
.
 平面
平面 ;
; 为直二面角,求直线
为直二面角,求直线 与平面
与平面 所成的角
所成的角 的正弦值.
的正弦值. ,把
,把 表示
表示 ,当
,当 时,
时, ;当
;当 时,
时, 为0或1. 记
为0或1. 记 为上述表示中
为上述表示中 ,
, ,
, ,
,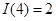 ),若
),若 ,
,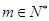 ,
, ,则(1)
,则(1) .
. .
. 的函数
的函数
 ;
; 使得
使得
 对一切自然数
对一切自然数 }满足
}满足 ,
,  ,并推测
,并推测