题目内容
在三棱柱ABC-A1B1C1中,∠ACB=120°,AC=CB=1,D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D.(1)若四边形CDD1C1总是矩形,求证:三棱柱ABC-A1B1C1为直三棱柱;
(2)在(1)的条件下,求二面角B-AD1-C的取值范围.

【答案】分析:(1)利用四边形CDD1C1总是矩形,证明CC1⊥平面ABC即可;
(2)求出平面BAD1、平面ACD1的一个法向量,再利用向量的夹角公式,我们可以求出二面角B-AD1-C的取值范围.
解答: (1)证明:∵D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D,四边形CDD1C1总是矩形,
(1)证明:∵D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D,四边形CDD1C1总是矩形,
∴CC1⊥平面ABC
∴三棱柱ABC-A1B1C1为直三棱柱…(5分);
(2)解:建立如图所示的直角坐标系,则A(0,- ,0),C(
,0),C( ,0,0),
,0,0),
设D(0,a,0),则D1(0,a,1),a∈[- ,
, ],
],
显然平面BAD1的一个法向量为 ,
,
设平面ACD1的一个法向量为
∵ ,
,
∴
∴
令x=1,∴y=-1,z=
∴平面ACD1的一个法向量 ,于是
,于是 ,
,
设二面角B-AD1-C的平面角为θ,∴cosθ= ═
═
∵ ,
, 2=2+(a+
2=2+(a+ )2∈[2,5],
)2∈[2,5],
∴cosθ∈[ ,
, ],
],
所以θ∈[arccos ,
, ]…(12分)
]…(12分)
点评:三棱柱为直棱柱的条件是侧棱与底面垂直,(2)问研究二面角的平面角,利用向量的方法,减少了辅助线的添加,将立体几何问题代数化,属于中档题.
(2)求出平面BAD1、平面ACD1的一个法向量,再利用向量的夹角公式,我们可以求出二面角B-AD1-C的取值范围.
解答:
 (1)证明:∵D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D,四边形CDD1C1总是矩形,
(1)证明:∵D1是线段A1B1上一动点(可以与A1或B1重合).过D1和CC1的平面与AB交于D,四边形CDD1C1总是矩形,∴CC1⊥平面ABC
∴三棱柱ABC-A1B1C1为直三棱柱…(5分);
(2)解:建立如图所示的直角坐标系,则A(0,-
 ,0),C(
,0),C( ,0,0),
,0,0),设D(0,a,0),则D1(0,a,1),a∈[-
 ,
, ],
],显然平面BAD1的一个法向量为
 ,
,设平面ACD1的一个法向量为

∵
 ,
,
∴

∴

令x=1,∴y=-1,z=

∴平面ACD1的一个法向量
 ,于是
,于是 ,
,设二面角B-AD1-C的平面角为θ,∴cosθ=
 ═
═
∵
 ,
, 2=2+(a+
2=2+(a+ )2∈[2,5],
)2∈[2,5],∴cosθ∈[
 ,
, ],
],所以θ∈[arccos
 ,
, ]…(12分)
]…(12分)点评:三棱柱为直棱柱的条件是侧棱与底面垂直,(2)问研究二面角的平面角,利用向量的方法,减少了辅助线的添加,将立体几何问题代数化,属于中档题.

练习册系列答案
相关题目
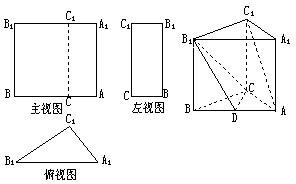 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.