题目内容
20.已知抛物线y2=4x的焦点F,准线为l,点P为抛物线上一点,且在第一象限,过P点作PA⊥l,垂足为A,|PF|=4,则$\overrightarrow{AF}$•$\overrightarrow{FP}$的值为-8.分析 利用抛物线的定义,|PF|=||PA|,设F在l上的射影为F′,依题意,可求得点P的坐标,从而可求得|AF′|,可求得点A的坐标,即可求出$\overrightarrow{AF}$•$\overrightarrow{FP}$的值.
解答 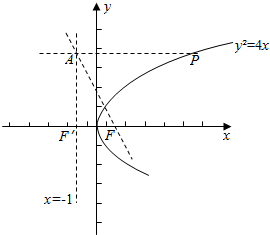 解:∵抛物线y2=4x的焦点为F,准线为l,
解:∵抛物线y2=4x的焦点为F,准线为l,
∴|PF|=||PA|,F(1,0),准线l的方程为:x=-1,
设F在l上的射影为F′,又PA⊥l,
设P(m,n),依|PF|=|PA|得,m+1=4,
解得m=3,n=2$\sqrt{3}$,
∵PA∥x轴,
∴点A的纵坐标为2$\sqrt{3}$,点A的坐标为(-1,2$\sqrt{3}$),
则$\overrightarrow{AF}$•$\overrightarrow{FP}$=(2,-2$\sqrt{3}$)•(2,2$\sqrt{3}$)=4-12=-8.
故答案为:-8.
点评 本题考查抛物线的定义、方程和简单性质,考查转化思想,考查解三角形的能力,属于中档题.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
15.函数f(x)=$\frac{x}{{x}^{2}+x+1}$的值域是( )
| A. | [-1,$\frac{1}{3}$) | B. | (-1,$\frac{1}{3}$] | C. | (-1,$\frac{1}{3}$) | D. | [-1,$\frac{1}{3}$] |
5.下列说法正确的是( )
| A. | 平行于同一向量的两个向量是共线向量 | |
| B. | 单位向量都相等 | |
| C. | $\overrightarrow{a}$∥$\overrightarrow{b}$?存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| D. | 与非零向量$\overrightarrow{a}$相等的向量有无数个 |