Question

4．设全集为U=R，集合A=（-∞，-3]∪[6，+∞），集合B=（-2，14）
（1）求如图阴影部分表示的集合；
（2）已知C={x|2a＜x＜a+1}，若C⊆B，求实数a的取值范围．

Answer 1

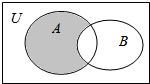
分析 （1）根据图形便可看出，阴影部分表示A∩B在A中的补集，用符号表示出来即可；
（2）C⊆B，从而C=∅时可以，并可求出对应的a的范围而C≠∅时；则a应满足$\left\{\begin{array}{l}{2a＜a+1}\\{2a≥-2}\\{a+1≤14}\end{array}\right.$，解出a的范围，再并上前面a的范围即可得到实数a的取值范围．

解答 解：（1）可以看出，阴影部分表示A，B交集在A中的补集，表示为：∁_A（A∩B）；
（2）①若C=∅，满足C⊆B，则：2a≥a+1；
∴a≥1；
②若C≠∅，则a满足：
$\left\{\begin{array}{l}{2a＜a+1}\\{2a≥-2}\\{a+1≤14}\end{array}\right.$；
解得-1≤a＜1；
∴a≥-1；
∴实数a的取值范围为[-1，+∞）．

点评 考查交集、补集的概念及其运算，空集的概念，以及子集的概念，不要漏了C=∅的情况．