题目内容
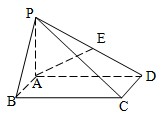 (2008•闸北区二模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,BC=2.
(2008•闸北区二模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,BC=2.(Ⅰ)求PC与平面PAD所成角的大小;
(Ⅱ)若E是PD的中点,求异面直线AE与PC所成角的大小;
(Ⅲ)在BC边上是否存在一点G,使得D点到平面PAG的距离为
| 2 |
分析:(Ⅰ)由题意可得:CD⊥PA,CD⊥AD,所以CD⊥平面APD,可得PC与平面PAD所成角既为∠CPD,再利用解三角形的有关知识即可求出答案.
(Ⅱ)设CD中点为F,连接EF,则EF∥PC,可得AE与EF所成角即为所求,然后利用解三角形的有关知识得到答案.
(Ⅲ)假设BC边上存在一点G满足题设条件,作DQ⊥AG,则DQ⊥平面PAG,可得DQ=
,进而得到BG=1,然后根据题意可得此点G符合题意.
(Ⅱ)设CD中点为F,连接EF,则EF∥PC,可得AE与EF所成角即为所求,然后利用解三角形的有关知识得到答案.
(Ⅲ)假设BC边上存在一点G满足题设条件,作DQ⊥AG,则DQ⊥平面PAG,可得DQ=
| 2 |
解答:解:(Ⅰ)因为PA⊥平面ABCD,CD?平面ABCD,
所以CD⊥PA,
又因为底面ABCD是矩形,
所以CD⊥AD,
所以由线面垂直的判定定理可得:CD⊥平面APD,
所以PC与平面PAD所成角既为∠CPD,….(2分)
又由题意可得:PD=
,CD=1
所以∠CPD=arctan
….(2分)
(Ⅱ)设CD中点为F,连接EF,则EF∥PC
所以AE与EF所成角即为所求….(1分)
又AE=
,EF=
PC=
,AF=
,
∴cos∠AEF=
=-
…(3分)
∴异面直线AE与PC所成角的大小为arccos
….(1分)
(Ⅲ)假设BC边上存在一点G满足题设条件,作DQ⊥AG,则DQ⊥平面PAG,
所以DQ=
….(3分)
∴BG=1<2,….(1分)
故存在点G,当BG=1时,使点D到平面PAG的距离为1….(1分)
所以CD⊥PA,
又因为底面ABCD是矩形,
所以CD⊥AD,
所以由线面垂直的判定定理可得:CD⊥平面APD,
所以PC与平面PAD所成角既为∠CPD,….(2分)
又由题意可得:PD=
| 5 |
所以∠CPD=arctan
| ||
| 5 |
(Ⅱ)设CD中点为F,连接EF,则EF∥PC
所以AE与EF所成角即为所求….(1分)
又AE=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴cos∠AEF=
| AE2+EF2-AF2 |
| 2AE•EF |
| ||
| 10 |
∴异面直线AE与PC所成角的大小为arccos
| ||
| 10 |
(Ⅲ)假设BC边上存在一点G满足题设条件,作DQ⊥AG,则DQ⊥平面PAG,
所以DQ=
| 2 |
∴BG=1<2,….(1分)
故存在点G,当BG=1时,使点D到平面PAG的距离为1….(1分)
点评:本题考查线面垂直的判定定理与空间中的线线角与线面角的有关知识,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角等问题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: