题目内容
学校艺术节举行学生书法、绘画、摄影作品大赛,某同学有A(书法)、B(绘画)、C(摄影)三件作品准备参赛,经评估,A作品获奖的概率为 ,B作品获奖的概率为
,B作品获奖的概率为 ,C作品获奖的概率为
,C作品获奖的概率为 .
.
(1)求该同学至少有两件作品获奖的概率;
(2)记该同学获奖作品的件数为ξ,求ξ的分布列和数学期望.
解:(1)该同学三件作品同时获奖的概率为 =
=
恰有两件作品获奖的概率为 +
+ +
+ =
=
故该同学至少有两件作品获奖的概率为 +
+ =
= ;
;
(2)由题意,ξ的所有可能取值为0,1,2,3,则
P(ξ=0)= =
= ,P(ξ=1)=
,P(ξ=1)= =
=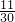 ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,
,
∴ξ的分布列为
∴Eξ=0× +1×
+1×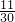 +2×
+2× +3×
+3× =
= .
.
分析:(1)该同学至少有两件作品获奖,包括三件作品同时获奖、恰有两件作品获奖,分别求概率,即可得到结论;
(2)确定变量的取值,求出相应的概率,即可求ξ的分布列和数学期望.
点评:本题考查互斥事件概率的求法,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.
 =
=
恰有两件作品获奖的概率为
 +
+ +
+ =
=
故该同学至少有两件作品获奖的概率为
 +
+ =
= ;
;(2)由题意,ξ的所有可能取值为0,1,2,3,则
P(ξ=0)=
 =
= ,P(ξ=1)=
,P(ξ=1)= =
=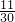 ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,
,∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  | 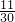 |  |  |
 +1×
+1×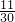 +2×
+2× +3×
+3× =
= .
.分析:(1)该同学至少有两件作品获奖,包括三件作品同时获奖、恰有两件作品获奖,分别求概率,即可得到结论;
(2)确定变量的取值,求出相应的概率,即可求ξ的分布列和数学期望.
点评:本题考查互斥事件概率的求法,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 ,B作品获奖的概率为
,B作品获奖的概率为 ,C作品获奖的概率为
,C作品获奖的概率为 .
.