题目内容
当x∈(1,2]时, (a>0)恒成立,则函数g(x)=lg(a2-a+3)的最小值是________.
(a>0)恒成立,则函数g(x)=lg(a2-a+3)的最小值是________.
lg
分析:先根据“当x∈(1,2]时, (a>0)恒成立”,求得a的取值范围,然后求出二次函数a2-a+3的最小值即可求出函数g(x)=lg(a2-a+3)的最小值.
(a>0)恒成立”,求得a的取值范围,然后求出二次函数a2-a+3的最小值即可求出函数g(x)=lg(a2-a+3)的最小值.
解答:设2x-1=t,则x=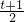 ,
,
∵x∈(1,2],∴t∈(1,3]
即 a< 恒成立,
恒成立,
因t∈(1,3]时,
 ,
, ,
,
∴0<a≤1;
又当a= 时,二次函数a2-a+3取最小值,且最小值为:
时,二次函数a2-a+3取最小值,且最小值为:
考虑到对数函数y=lgx是增函数,
则函数g(x)=lg(a2-a+3)的最小值是lg
故答案为:lg
点评:本题主要考查函数恒成立问题、对数函数的单调性与特殊点,以及转化思想的应用和计算能力,属于对知识和思想方法的综合考查,属于中档题.

分析:先根据“当x∈(1,2]时,
 (a>0)恒成立”,求得a的取值范围,然后求出二次函数a2-a+3的最小值即可求出函数g(x)=lg(a2-a+3)的最小值.
(a>0)恒成立”,求得a的取值范围,然后求出二次函数a2-a+3的最小值即可求出函数g(x)=lg(a2-a+3)的最小值.解答:设2x-1=t,则x=
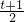 ,
,∵x∈(1,2],∴t∈(1,3]
即 a<
 恒成立,
恒成立,因t∈(1,3]时,
 ,
, ,
,∴0<a≤1;
又当a=
 时,二次函数a2-a+3取最小值,且最小值为:
时,二次函数a2-a+3取最小值,且最小值为:
考虑到对数函数y=lgx是增函数,
则函数g(x)=lg(a2-a+3)的最小值是lg

故答案为:lg

点评:本题主要考查函数恒成立问题、对数函数的单调性与特殊点,以及转化思想的应用和计算能力,属于对知识和思想方法的综合考查,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目