已知log23=t.则log4854=$\frac{1+3t}{4+t}$ 题目和参考答案——青夏教育精英家教网——

题目内容

8．已知log₂3=t，则log₄₈54=$\frac{1+3t}{4+t}$（用t表示）

分析利用对数的换底公式化简求解即可．

解答解：log₂3=t，则log₄₈54=$\frac{lo{g}_{2}54}{lo{g}_{2}48}$=$\frac{1+3lo{g}_{2}3}{4+lo{g}_{2}3}$=$\frac{1+3t}{4+t}$．
故答案为：$\frac{1+3t}{4+t}$．

点评本题考查换底公式的应用，对数运算法则的应用，考查计算能力．

练习册系列答案

小升初集结号系列答案

名著导读全析精练系列答案

学科教学基本要求系列答案

寒假学习与应用系列答案

活动填图册系列答案

有效课堂精讲精练系列答案

新课程初中物理同步训练系列答案

单元测评四川教育出版社系列答案

锁定100分小学毕业模考卷系列答案

相关题目

16．设α，β，γ∈（0，$\frac{π}{2}$），且sinα+sinγ=sinβ，cosα-cosγ=cosβ，则α-β的值为（　　）

-$\frac{π}{3}$

$\frac{π}{3}$或-$\frac{π}{3}$

19．已知命题p：若x＞y，则|x|＞|y|；命题q：若x+y=0，则x=-y．有命题①p∧q；②p∨q；③p∧（￢q）；④（￢p）∨q．其中真命题是（　　）

16．执行如图所示程序框图，输出的a=（　　）

3．已知α∈（0，$\frac{π}{2}$），β∈（-$\frac{π}{2}$，0），cos（$α+\frac{π}{4}$）=$\frac{1}{3}$，cos（$\frac{β}{2}-\frac{π}{4}$）=$\frac{\sqrt{3}}{3}$，则cos（$α+\frac{β}{2}$）=（　　）

$\frac{5}{9}\sqrt{3}$

-$\frac{\sqrt{6}}{9}$

$\frac{\sqrt{3}}{3}$

-$\frac{\sqrt{3}}{3}$

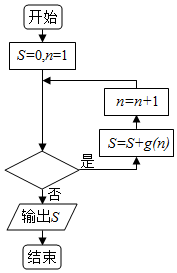已知函数f（x）=ax³+$\frac{1}{2}$x²在x=-1处取得极大值，记g（x）=$\frac{1}{f′（x）}$．在如图所示的程序框图中，若输出的结果S=$\frac{2016}{2017}$，则判断框中可以填入的关于n的判断条件是（　　）

20．若复数z满足z（1+i）=|1+$\sqrt{3}$i|，则在复平面内z的共轭复数对应的点位于（　　）

17．定义在区间[x₁，x₂]上的函数y=f（x）的图象为C，M是C上任意一点，O为坐标原点，设向量$\overrightarrow{OA}=（{{x_1}，f（{x_1}）}），\overrightarrow{OB}=（{{x_2}，f（{x_2}）}），\overrightarrow{OM}=（{x，y}）$，且实数λ满足x=λx₁+（1-λ）x₂，此时向量$\overrightarrow{ON}=λ\overrightarrow{OA}+（{1-λ}）\overrightarrow{OB}$．若$|{\overrightarrow{MN}}$|≤K恒成立，则称函数y=f（x）在区间[x₁，x₂]上可在标准K下线性近似，其中K是一个确定的实数．已知函数f（x）=x²-2x在区间[1，2]上可在标准K下线性近似，那么K的最小值是$\frac{1}{4}$．

18．（Ⅰ）已知$f（α）=\frac{sin（π-α）cos（2π-α）tan（-α+π）}{tan（-π-α）sin（-π-α）}$，若α是第三象限角，且$cos（{α-\frac{3π}{2}}）=\frac{{2\sqrt{6}}}{5}$，求f（α）的值
（Ⅱ）已知$α，β∈（0，\frac{π}{4}），且3sinβ=sin（2α+β），\begin{array}{l}{\;}{4tan\frac{α}{2}=1-{{tan}^2}}\end{array}\frac{α}{2}$，求α+β的值．