题目内容
函数y=f（x）是偶函数，y=f（x-2）在[0，2]上单调递增，则f（-1），f（0），f（2）的大小关系是 ________．
解：∵f（x）是偶函数，∴其图象关于y轴对称，
又∵y=f（x-2）的图象是由y=f（x）向右平移2个单位得到的，
而y=f（x-2）在[0，2]上单调递增，
∴f（x）在[-2，0]上单调递增，在[0，2]上单调递减，
∴f（-1）=f（1）且f（0）＞f（1）＞f（2），
∴其大小关系为f（0）＞f（-1）＞f（2）．
故答案为：f（0）＞f（-1）＞f（2）
分析：由f（x）是偶函数，可知其图象关于y轴对称，再由y=f（x-2）的图象是由y=f（x）向右平移2个单位得到的，而y=f（x-2）在[0，2]上单调递增，可得到f（x）在[-2，0]上单调递增，在[0，2]上单调递减，从而得到结论．
点评：本题主要考查函数的奇偶性与单调性的综合应用，即：奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相异．
又∵y=f（x-2）的图象是由y=f（x）向右平移2个单位得到的，
而y=f（x-2）在[0，2]上单调递增，
∴f（x）在[-2，0]上单调递增，在[0，2]上单调递减，
∴f（-1）=f（1）且f（0）＞f（1）＞f（2），
∴其大小关系为f（0）＞f（-1）＞f（2）．
故答案为：f（0）＞f（-1）＞f（2）
分析：由f（x）是偶函数，可知其图象关于y轴对称，再由y=f（x-2）的图象是由y=f（x）向右平移2个单位得到的，而y=f（x-2）在[0，2]上单调递增，可得到f（x）在[-2，0]上单调递增，在[0，2]上单调递减，从而得到结论．
点评：本题主要考查函数的奇偶性与单调性的综合应用，即：奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相异．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
读图分析解答：设定义在闭区间[-4，4]上的函数y=f（x）的图象如图所示（图中坐标点都是实心点），完成以下几个问题：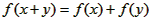
，
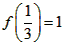，且当x>0时，f（x）>0。 
，求x的取值范围。