题目内容
设函数y=f(x)是定义域在R,并且满足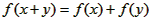 ,
,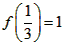 ,且当x>0时,f(x)>0。
,且当x>0时,f(x)>0。
(1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果 ,求x的取值范围。
,求x的取值范围。
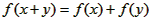 ,
,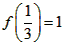 ,且当x>0时,f(x)>0。
,且当x>0时,f(x)>0。 (1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果
 ,求x的取值范围。
,求x的取值范围。 解:(1)令x=y=0,则f(0)=f(0)+f(0),
∴f(0)=0;
(2)令y=-x,得
 ,
,
故函数f(x)是R上的奇函数
(3)任取 ,则
,则

 ,
,
故f(x)是R上的增函数
∵ ∴
∴
∴ ,
,
又由y=f(x)是定义在R上的增函数,
得 ,解之得
,解之得 ,
,
故
∴f(0)=0;
(2)令y=-x,得

 ,
,故函数f(x)是R上的奇函数
(3)任取
 ,则
,则

 ,
,故f(x)是R上的增函数
∵
 ∴
∴
∴
 ,
,又由y=f(x)是定义在R上的增函数,
得
 ,解之得
,解之得 ,
,故


练习册系列答案
相关题目