题目内容
|
(1)求证:M点的坐标为(1,0);
(2)求证:![]() ;
;
(3)求![]() 的面积的最小值.
的面积的最小值.
(1)证明:设![]() 与
与![]() 联立得:
联立得:![]() ①
①
![]() 为①的两根,
为①的两根,![]() ,
,![]()
![]() 点的坐标为(1,0);
点的坐标为(1,0);
(法二):也可分斜率k存在或k不存在两种情况讨论(k=0不合题意)
当斜率k存在时,设![]() 与
与![]() 联立得:
联立得:![]()
![]()
![]()
![]() 当y=0时,x=1
当y=0时,x=1![]()
![]() 点的坐标为(1,0);
点的坐标为(1,0);
当斜率k不存在时,设![]() ,与
,与![]() 联立得
联立得![]()
![]() 也过此点.
也过此点.
(2)证明:![]() ,
,![]() .
.
(3)![]()
![]()
当且仅当![]() 时,
时,![]() 的面积取最小值为1。
的面积取最小值为1。
(法二):也可![]()
![]()
当且仅当![]() ,即
,即![]() 时,
时,![]() 的面积取最小值为1。
的面积取最小值为1。

练习册系列答案
相关题目
 中,
中, ,
,  ,若
,若 是
是 中点.
中点. ∥平面
∥平面 ;
; 所成的角.
所成的角.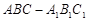 中,△
中,△ 为等腰直角三角形,∠
为等腰直角三角形,∠ =
= ,且
,且 =
=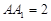 ,
, 、
、 、
、 分别为
分别为 、
、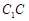 、
、 的中点.
的中点.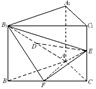
 ∥平面
∥平面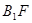 ⊥平面
⊥平面 ;
; 的体积.
的体积. 中,
中,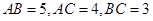 ,
, ,点
,点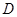 在
在 上.
上.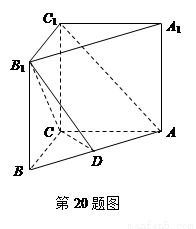
 ∥平面
∥平面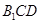 ;
;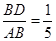 时,求二面角
时,求二面角 的余弦值.
的余弦值. 中,
中, 为等腰直角三角形,
为等腰直角三角形, ,且
,且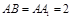 ,D,E,F分别为
,D,E,F分别为 的中点,
的中点,
 //平面
//平面 ;
; 平面
平面 ;
; 到平面
到平面 的距离。
的距离。