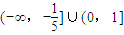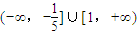题目内容
a是实常数,函数f(x)对于任何的非零实数x都有f(
)=af(x)-x-1,且f(1)=1,则不等式f(x)-x≥0的解集为( )
| 1 |
| x |
A.(-∞,-
| B.(-∞,-
| ||||
C.[-
| D.[-
|
因为f(1)=1,所以f(1)=af(1)-2,即a-2=1,解得a=3,
所以f(
)=3f(x)-x-1①,
设
=t,得到f(t)=3f(
)-
-1,即f(x)=3f(
)-
-1②,
将①代入②得:f(x)=3[3f(x)-x-1]-
-1,
化简得:f(x)=
+
+
,
代入不等式得:
+
+
-x≥0,
当x>0时,去分母得:5x2-4x-1≤0,即(5x+1)(x-1)≤0,
解得:-
≤x≤1,所以原不等式的解集为(0,1];
当x<0时,去分母得:5x2-4x-1≥0,即(5x+1)(x-1)≥0,
解得:x≥1或x≤-
,所以原不等式的解集为(-∞,-
],
综上,原不等式的解集为(-∞,-
]∪(0,1].
故选A
所以f(
| 1 |
| x |
设
| 1 |
| x |
| 1 |
| t |
| 1 |
| t |
| 1 |
| x |
| 1 |
| x |
将①代入②得:f(x)=3[3f(x)-x-1]-
| 1 |
| x |
化简得:f(x)=
| 3x |
| 8 |
| 1 |
| 8x |
| 1 |
| 2 |
代入不等式得:
| 3x |
| 8 |
| 1 |
| 8x |
| 1 |
| 2 |
当x>0时,去分母得:5x2-4x-1≤0,即(5x+1)(x-1)≤0,
解得:-
| 1 |
| 5 |
当x<0时,去分母得:5x2-4x-1≥0,即(5x+1)(x-1)≥0,
解得:x≥1或x≤-
| 1 |
| 5 |
| 1 |
| 5 |
综上,原不等式的解集为(-∞,-
| 1 |
| 5 |
故选A

练习册系列答案
相关题目
a是实常数,函数f(x)对于任何的非零实数x都有f(
)=af(x)-x-1,且f(1)=1,则不等式f(x)-x≥0的解集为( )
| 1 |
| x |
A、(-∞,-
| ||
B、(-∞,-
| ||
C、[-
| ||
D、[-
|
 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )



 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )



 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )