题目内容
已知F1、F2是平面α内的定点，并且|F1F2|=2c(c＞0),M是α内的动点,且|MF1|+|MF2|=2a，判断动点M的轨迹.
解:(1)当2a＞2c，即a＞c时，动点M到两定点的距离之和大于两定点之间的距离，由椭圆的定义知动点M的轨迹是以F1、F2为焦点的椭圆.
(2)当2a=2c即a=c时，动点M到两定点F1、F2的距离之和等于线段F1F2的长，所以点M是线段F1F2上的点.所以动点M的轨迹是线段F1F2.
综上所述，当a＞c时，动点的轨迹是椭圆，当a=c时，动点的轨迹是线段.
练习册系列答案
相关题目
已知F1、F2是椭圆
+
=1的两个焦点，平面内一个动点M满足|MF1|-|MF2|=2，则动点M的轨迹是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、双曲线 | B、双曲线的一个分支 |
| C、两条射线 | D、一条射线 |
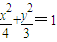的两个焦点，平面内一个动点M满足|MF1|-|MF2|=2，则动点M的轨迹是（ ）