题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若方程
时,若方程![]() 在
在![]() 上总有两个不等的实根, 求
上总有两个不等的实根, 求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() . (2)
. (2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据导数的几何意义得到参数值;(2)不等式![]() 恒成立,即
恒成立,即![]() ,
,
等价于![]() ,令
,令![]() ,对这个函数求导研究单调性求最值即可;(3)
,对这个函数求导研究单调性求最值即可;(3)![]() 即
即![]() ,
,![]() ,令
,令![]() ,对这个函数求导研究函数的单调性,求得函数的变化趋势,使得函数和x轴有两个不同的交点即可.
,对这个函数求导研究函数的单调性,求得函数的变化趋势,使得函数和x轴有两个不同的交点即可.
解析:(Ⅰ) ![]() ,
,![]() .
.
(Ⅱ)当![]() 时,
时,![]() .
. ![]() (
(![]() ).所以
).所以![]() 即
即![]() .
.
又因为![]() ,所以
,所以![]() 等价于
等价于![]() .
.
令![]() ,则
,则![]() .解
.解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,所以
单调递减,所以![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]()
(Ⅲ)当![]() 时,
时,![]() 即
即![]() ,
,![]() .
.
令![]() ,则
,则![]() .
.
方程![]() 在
在![]() 上总有两个不等的实根等价于
上总有两个不等的实根等价于
函数![]() 的图象与
的图象与![]() 轴在
轴在![]() 上有两个不同的交点.
上有两个不同的交点.
(ⅰ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 单调递减,
单调递减,
从而函数![]() 在
在![]() 内的零点最多一个,不符合题意.
内的零点最多一个,不符合题意.
(ⅱ)当![]() 时,因为
时,因为![]() ,
,
解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() ;解
;解![]() ,得
,得![]() .
.
所以函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() 当
当![]() 时,
时,![]() 在
在![]() 单调递减,函数
单调递减,函数![]() 在区间
在区间![]() 内的零点最多一个,不符
内的零点最多一个,不符
②当![]() 时,因为当
时,因为当![]() 趋于
趋于![]() 时,
时,![]() 的值趋于正无穷大,
的值趋于正无穷大,
所以当且仅当![]() 时函数
时函数![]() 在
在![]() 有两个零点.
有两个零点.
由![]() 得
得![]() ,即
,即![]() 对
对![]() 恒成立. 等价于
恒成立. 等价于![]() .
.
再令![]() ,则
,则![]() .
.
解![]() 得
得![]() ;解
;解![]() 得
得![]() ;解
;解![]() 得
得![]() .
.
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
所以![]() ,故
,故![]() 的解为
的解为![]() .
.
由![]() 得
得![]() 即
即![]() 对
对![]() 恒成立.所以
恒成立.所以![]() ,
,
所以![]() 的解为
的解为![]() .所以
.所以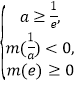 的解为
的解为![]() . 综合①②得
. 综合①②得![]() .
.
综合(ⅰ)(ⅱ)得满足题意要求的实数![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
