题目内容
【题目】如图是一矩形滨河公园![]() ,其中
,其中![]() 长为
长为![]() 百米,
百米,![]() 长为
长为![]() 百米,
百米,![]() 的中点
的中点![]() 为便民服务中心.根据居民实际需求,现规划建造三条步行通道
为便民服务中心.根据居民实际需求,现规划建造三条步行通道![]() 、
、![]() 及
及![]() ,要求点
,要求点![]() 、
、![]() 分别在公园边界
分别在公园边界![]() 、
、![]() 上,且
上,且![]() .
.

(1)设![]() .①求步道总长度
.①求步道总长度![]() 关于
关于![]() 的函数解析式
的函数解析式![]() ;②求函数
;②求函数![]() 的定义域.
的定义域.
(2)为使建造成本最低,需步行通道总长最短,试求步行通道总长度的最小值.
【答案】(1)①![]() .,②
.,②![]() ;(2)
;(2)![]() 百米.
百米.
【解析】
(1)①根据![]() ,
,![]() ,得到
,得到![]() ,然后分别在
,然后分别在![]() 中,用余弦函数的定义得到
中,用余弦函数的定义得到![]() ,在
,在![]() 中,用正弦函数的定义得到
中,用正弦函数的定义得到![]() ,在
,在![]() 中,用勾股定理得到
中,用勾股定理得到![]() ,然后相加即可,②根据
,然后相加即可,②根据![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在公园边界
分别在公园边界![]() 、
、![]() 上,则有
上,则有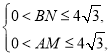 求解.
求解.
(2)由(1)的结论,![]() .令
.令![]() ,转化为
,转化为![]() ,利用反比例函数的单调性求解.
,利用反比例函数的单调性求解.
(1)①在矩形![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
在![]() 中,
中,
![]() ,
,![]() .
.
又因为![]() ,
,
所以![]() ,
,
所以![]() .
.
②因为![]() ,
,![]() ,
,
所以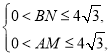 即
即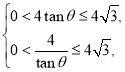
解得![]() ,所以
,所以![]() ,
,
所以函数![]() 的定义域为
的定义域为![]() .
.
(2)![]() .
.
令![]() ,
,
则![]() ,
,
所以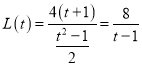 .
.
因为![]() ,所以
,所以![]() ,
,
所以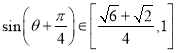 ,
,
所以 .
.
因为![]() 在
在 上为减函数,
上为减函数,
所以当![]() ,即
,即![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
故步行通道总长度的最小值为![]() 百米.
百米.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目