Question

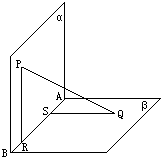
在直二面角α-PQ-β中，直角三角形ABC在面α内，斜边AB在棱PQ上，若AC与面β成30°的角，则BC与面β所成角为

1. A.
   30°
2. B.
   45°
3. C.
   60°
4. D.
   60°或120°

Answer 1

C
分析：作CD⊥AB，根据面面垂直的性质定理可知CD⊥β，从而∠CAB=30°，可求出∠CBA，而∠CBA即为BC与面β所成角，从而求出所求．
解答：作CD⊥AB，
∵直二面角α-PQ-β
∴CD⊥β
∵AC与面β成30°的角
∴∠CAB=30°
又因直角三角形ABC
∴∠CBA=60°
而∠CBA即为BC与面β所成角
故选C．
点评：本题主要考查了与二面角有关的立体几何综合题，以及直线与平面所成的角，解题的关键是画图理解题意，属于中档题．