题目内容
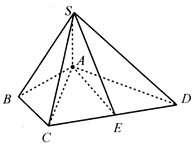
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求这个六面体
,求这个六面体![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】
(1)由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,由面面垂直的性质可得结果;(2)以
,由面面垂直的性质可得结果;(2)以![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立平面直角坐标系,设
轴建立平面直角坐标系,设![]() ,利用向量垂直数量积为零列方程求出平面
,利用向量垂直数量积为零列方程求出平面![]() 的一个法向量与平面
的一个法向量与平面![]() 的一个法向量,利用空间向量夹角余弦公式,列方程可求得
的一个法向量,利用空间向量夹角余弦公式,列方程可求得![]() ,由棱锥的体积公式可得结果.
,由棱锥的体积公式可得结果.
(Ⅰ)在梯形![]() 中,∵
中,∵![]() ,
,![]() ,
,
 ∴
∴![]()
![]() ,
,
∴![]()
![]() ,∵
,∵![]() .
.
∴![]()
![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,
中,![]()
![]()
![]() ,∴
,∴![]() .
.
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立平面直角坐标系, 设
轴建立平面直角坐标系, 设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,![]() ,易知平面
,易知平面![]() 的一个法向量为
的一个法向量为![]() ,设
,设
∵平面![]() 的法向量为
的法向量为![]() ,∴
,∴ 即
即![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的法向量为
的法向量为![]() ,∵二面角
,∵二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,
,
∴![]()
![]()
![]() ,解得
,解得![]() ,即
,即![]() .
.
所以六面体![]() 的体积为:
的体积为:
![]()
![]()
![]()
![]()
![]()
![]() .
.

练习册系列答案
相关题目
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如表1所示.
表1
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到积极参加班级工作的学生的概率是多少?抽到不积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.
参考表2
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| 0.05 | 0.005 | 0.001 | ||
| 3.841 | 6.635 | 7.879 | 10.8 |