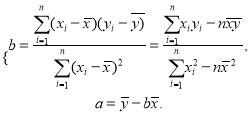题目内容
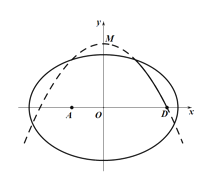
【题目】学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() .观测点
.观测点![]() 实时跟踪航天器.
实时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程(只需求出曲线方程即可,不必求范围);
(2)试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() 测得离航天器的距离为多少时,应向航天器发出变轨指令?
测得离航天器的距离为多少时,应向航天器发出变轨指令?
【答案】(1)![]() ;(2)10
;(2)10
【解析】
(1)先设出抛物线的方程,结合所经过的点列出方程,然后解方程得到参数的值;
(2)先求解变轨时点的坐标,然后利用两点间的距离公式求出![]() 即可.
即可.
(1)设曲线方程为![]() ,由题意可知,
,由题意可知,![]() ,
,
∴![]() ,
,
∴曲线方程为![]() ;
;
(2)设变轨点为![]() ,根据题意可知
,根据题意可知 ,得
,得![]() ,解得
,解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ,得
,得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,
答:当观测点![]() 测得离航天器的距离为10时,应向航天器发出变轨指令.
测得离航天器的距离为10时,应向航天器发出变轨指令.

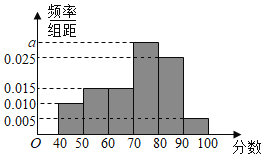
【题目】某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | 0.10 |
三组 | 10≤t<15 | 10 | ② |
四组 | 15≤t<20 | ① | 0.50 |
五组 | 20≤t≤25 | 30 | 0.30 |
合计 | 100 | 1.00 |

解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
【题目】
随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 5 | 6 | 7 | 8 | 10 |
(Ⅰ)求y关于t的回归方程![]()
(Ⅱ)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中