题目内容

已知双曲线 $数学公式$ 的离心率为 $数学公式$ ，顶点与椭圆 $数学公式$ 的焦点相同，那么该双曲线的焦点坐标为，渐近线方程为．

$\text{[math]}$ $\text{[math]}$
分析：求得椭圆的焦点，求得双曲线的顶点，从而可得几何量，即可求得双曲线的焦点坐标、渐近线方程．
解答：∵椭圆 $\text{[math]}$ 的焦点为（± $\text{[math]}$ ，0）
∴双曲线的顶点为（± $\text{[math]}$ ，0），离心率为 $\text{[math]}$ ，
∴a= $\text{[math]}$ ， $\text{[math]}$ ，
∴c=2 $\text{[math]}$ ，∴b= $\text{[math]}$ = $\text{[math]}$
∴该双曲线的焦点坐标为 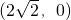$\text{[math]}$ ，渐近线方程为 $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查椭圆、双曲线的几何性质，考查双曲线的标准方程，属于基础题．

练习册系列答案

加分猫汇练系列答案

金博士1课3练单元达标测试题系列答案

小学目标测试系列答案

新编小学单元自测题系列答案

走向重点中考标准模拟冲刺卷系列答案

走进英语小屋系列答案

总复习测试卷系列答案

综合学习与评估系列答案

综合能力训练系列答案

字词句段篇系列答案

相关题目

已知双曲线的离心率为2，焦点是（-4，0），（4，0），则双曲线方程为（　　）

已知双曲线的离心率为2，F₁、F₂是左右焦点，P为双曲线上一点，且∠F₁PF₂=60°，S△PF1F2=12

．该双曲线的标准方程为

已知双曲线的离心率为2，焦点是（-4，0），（4，0），则双曲线方程为

（本小题满分12分）

已知双曲线的离心率为2，焦点到渐近线的距离等于，过右焦点的直线

交双曲线于、两点，为左焦点，

（Ⅰ）求双曲线的方程；

（Ⅱ）若的面积等于，求直线的方程．

已知双曲线的离心率为2，焦点到渐近线的距离为，点P的坐标为（0，－2），过P的直线l与双曲线C交于不同两点M、N.

（1）求双曲线C的方程；

（2）设（O为坐标原点），求t的取值范围