题目内容

在三棱柱ABC-A1B1C1中，P，Q分别是AB1与A1C的中点，如图．求证：PQ∥面ABC
分析：欲证PQ∥面ABC，只需证明PQ垂直平面ABC上的一条直线，利用中点，得到三角形A1BC的中位线PQ∥BC，而BC为平面ABC上的一条直线，问题得证．
解答：解：连接A1B
∵A1B1BA为平行四边形，P为AB1的中点
∴A1B∩AB1=P
∴P为A1B的中点
又∵Q为A1C的中点
∴PQ∥BC
又∵PQ?面ABC，BC?面ABC
∴PQ∥面ABC
点评：本题主要考查了直线与平面平行的判定，关键是在平面中寻找与已知直线平行的直线．
练习册系列答案
相关题目
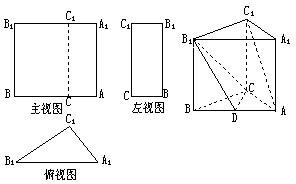精英家教网已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，cos∠A1=
35
．
（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）在三棱柱ABC-A1B1C1中，若D是底边AB的中点，求证：AC1∥平面CDB1．
（3）若三棱柱的高为5，求三视图中左视图的面积．
精英家教网如图：在正三棱柱ABC-A1 B1 C1中，AB=
AA13
=a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．
（Ⅰ）求证：面AEF⊥面ACF；
（Ⅱ）求三棱锥A1-AEF的体积．
在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）求点C到平面A1ABB1的距离；
（2）求二面角A-BC1-B1的余弦值；
（3）若M，N分别为直线AA1，B1C上动点，求MN的最小值．
（2012•江西）在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=
5
，BC=4，在A1在底面ABC的投影是线段BC的中点O．
（1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
（2）求平面A1B1C与平面BB1C1C夹角的余弦值．
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
BDBC1
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网