题目内容
正四棱锥相邻侧面所成的角为α,侧面与底面所成的角为β,则2cosα+cos2β的值是( )A.-1
B.1
C.

D.2
【答案】分析:设正四棱锥S-ABCD的底面边长为a,侧棱长为b,作出两个二面角的平面角,利用勾股定理、余弦定理和二倍角的余弦公式等解三角形的知识求解即可.
解答: 解:设正四棱锥S-ABCD的底面边长为a,侧棱长为b,如图
解:设正四棱锥S-ABCD的底面边长为a,侧棱长为b,如图
过S做SE⊥AB与E,SO⊥底面ABCD与O,连EO,则∠SEO即为侧面与底面所成二面角的平面角,即为β,
在三角形SEO中,SE2= ,OE=
,OE= ,
,
∴cos2β= ,cos2β=2cos2β-1=
,cos2β=2cos2β-1= ,
,
过B做BH⊥SA与H,连CH,由△SAB≌△SAC,所以CH⊥SA,则角BHC即为两个侧面所成的二面角的平面角,即α,
在△BCH中,BC=a,BH=CH= ,
,
由余弦定理可得cosα= ,
,
∴2cosα+cos2β=2(cosα+cos2β )-1=0-1=-1
故选A
点评:本题考查二面角的做法和求解、勾股定理、余弦定理和二倍角的余弦公式等解三角形知识,考查空间想象能力和运算能力.
解答:
 解:设正四棱锥S-ABCD的底面边长为a,侧棱长为b,如图
解:设正四棱锥S-ABCD的底面边长为a,侧棱长为b,如图过S做SE⊥AB与E,SO⊥底面ABCD与O,连EO,则∠SEO即为侧面与底面所成二面角的平面角,即为β,
在三角形SEO中,SE2=
 ,OE=
,OE= ,
,∴cos2β=
 ,cos2β=2cos2β-1=
,cos2β=2cos2β-1= ,
,过B做BH⊥SA与H,连CH,由△SAB≌△SAC,所以CH⊥SA,则角BHC即为两个侧面所成的二面角的平面角,即α,
在△BCH中,BC=a,BH=CH=
 ,
,由余弦定理可得cosα=
 ,
,∴2cosα+cos2β=2(cosα+cos2β )-1=0-1=-1
故选A
点评:本题考查二面角的做法和求解、勾股定理、余弦定理和二倍角的余弦公式等解三角形知识,考查空间想象能力和运算能力.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 ,则
,则 ;
;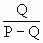 ;
;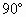 .
. ,侧面与底面所成的角为
,侧面与底面所成的角为 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.