题目内容
20. 已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动(Ⅰ)经过1小时后,甲、乙两小船相距多少海里?
(Ⅱ)在航行过程中,小船甲是否可能处于小船乙的正东方向?若可能,请求出所需时间,若不可能,请说明理由.
分析 (Ⅰ)利用余弦定理求|EF|的长度即可.
(Ⅱ)设经过t(0<t<5)小时小船甲处于小船乙的正东方向.利用正弦定理建立条件关系进行求解即可.
解答 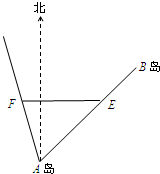 解:(Ⅰ)经过1小时后,甲船到达E点,乙船到达F点,
解:(Ⅰ)经过1小时后,甲船到达E点,乙船到达F点,
|AE|=10-2=8,|AF|=2,∠EAF=60°,┅┅┅┅┅┅┅┅┅┅┅┅┅2分
∴|EF|2=|AE|2+|AF|2-2|AE||AF|cos60°=64+4-2×$8×2×\frac{1}{2}$=52,
∴|EF|=2$\sqrt{13}$.┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
(Ⅱ)设经过t(0<t<5)小时小船甲处于小船乙的正东方向.
则甲船与A距离为|AE|=10-2t海里,乙船与A距离为|AF|=2t海里,∠EAF=60°,∠EFA=45°,┅┅┅6分
则由正弦定理得$\frac{|AE|}{sin45°}$=$\frac{|AF|}{sin75°}$,
即$\frac{2t}{sin45°}=\frac{10-2t}{sin75°}$,┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
则t=$\frac{10sin45°}{2sin75°+2sin45°}$=$\frac{10}{3+\sqrt{3}}$<5.┅┅┅┅┅┅┅┅11分
答:经过$\frac{10}{3+\sqrt{3}}$小时小船甲处于小船乙的正东方向.┅┅┅┅┅┅┅┅┅12分.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理建立方程关系是解决本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
10.已知三棱锥的三视图如图所示,则它的外接球的体积为( )


| A. | π | B. | 4π | C. | $\frac{2π}{3}$ | D. | $\frac{4π}{3}$ |
15.椭圆$\frac{x^2}{36}+\frac{y^2}{9}=1$的弦被点(4,2)平分,则此弦所在的直线方程是( )
| A. | x-2y=0 | B. | x+2y=4 | C. | 2x+3y=14 | D. | x+2y=8 |
5.在△ABC中,若C=$\frac{π}{4}$,a=6,B=$\frac{π}{6}$,则ab等于( )
| A. | 36$\sqrt{3}$+36 | B. | 6$\sqrt{3}$+6 | C. | 3$\sqrt{6}-3\sqrt{2}$ | D. | 18$\sqrt{6}-18\sqrt{2}$ |
9.随机变量X的概率分布如下,则P(X≤1)=0.4.
| X | 0 | 1 | 2 | 3 |
| P | 0.3 | m | 0.5 | 0.1 |
10.设m,n是两条不同的直线,α,β是两个不同的平面( )
| A. | 若m⊥n,n∥α,则m⊥α | B. | 若m∥β,β⊥α则m⊥α | ||
| C. | 若m∥n,n⊥α则m⊥α | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
 正方体ABCD-A1B1C1D1中,异面直线B1C与C1D所成的角的大小为60°.
正方体ABCD-A1B1C1D1中,异面直线B1C与C1D所成的角的大小为60°. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.