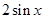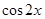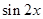题目内容
已知函数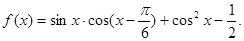
(1)求函数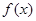 的最大值,并写出
的最大值,并写出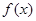 取最大值
取最大值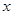 时的取值集合;
时的取值集合;
(2)在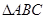 中,角
中,角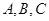 的对边分别为
的对边分别为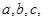 ,若
,若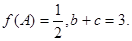 求
求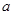 的最小值.
的最小值.
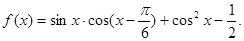
(1)求函数
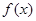 的最大值,并写出
的最大值,并写出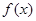 取最大值
取最大值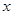 时的取值集合;
时的取值集合;(2)在
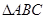 中,角
中,角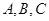 的对边分别为
的对边分别为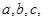 ,若
,若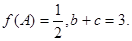 求
求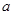 的最小值.
的最小值.(1) ,
, (2)
(2)
 ,
, (2)
(2)
试题分析:(1)研究三角函数性质,首先将其化为基本三角函数形式,即
 .利用两角和与差余弦公式、二倍角公式、配角公式,化简得
.利用两角和与差余弦公式、二倍角公式、配角公式,化简得
 ,再结合三角函数基本性质,可得函数
,再结合三角函数基本性质,可得函数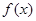 的最大值为
的最大值为 .
.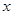 的取值集合为
的取值集合为 .(2)解三角形问题,利用正余弦定理进行边角转化. 因为
.(2)解三角形问题,利用正余弦定理进行边角转化. 因为 ,所以
,所以 已知一角及两夹边,利用余弦定理得
已知一角及两夹边,利用余弦定理得 .结合基本不等式,可得
.结合基本不等式,可得 .
.试题解析:(1)

 .
.∴函数
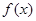 的最大值为
的最大值为 .当
.当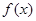 取最大值时
取最大值时
 ,解得
,解得 .
.故
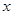 的取值集合为
的取值集合为 . (6分)
. (6分)(2)由题意
 ,化简得
,化简得 
 ,
, , ∴
, ∴ , ∴
, ∴
在
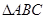 中,根据余弦定理,得
中,根据余弦定理,得 .
.由
 ,知
,知 ,即
,即 .
.∴当
 时,
时,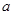 取最小值
取最小值 . (12分)
. (12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
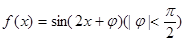 的图象向左平移
的图象向左平移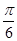 个单位后关于原点对称,则函
个单位后关于原点对称,则函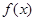 在
在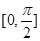 上的最小值为( )
上的最小值为( )



 ,则方程
,则方程 的解是_____________.
的解是_____________.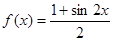 ,若
,若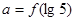 ,
,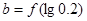 则下列正确的是( )
则下列正确的是( )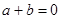
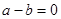

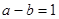
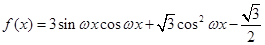 ,其中
,其中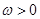 .若
.若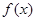 在区间
在区间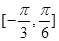 上为增函数,则
上为增函数,则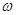 的最大值为( )
的最大值为( )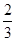
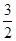
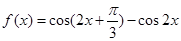 ,其中
,其中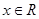 ,给出下列四个结论
,给出下列四个结论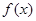 是最小正周期为
是最小正周期为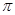 的奇函数;
的奇函数;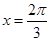 ;
;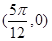 ;
;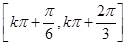 ,
,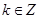 .
.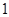 个
个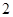 个
个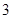 个
个 个
个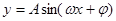 在一个周期内的图象如右,此函数的解析式为( )
在一个周期内的图象如右,此函数的解析式为( )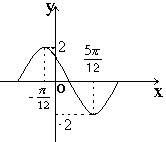
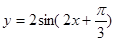 B.
B.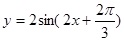
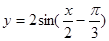 D.
D.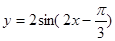
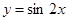 的图象向右平移
的图象向右平移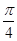 个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )
个单位,再向上平移1个单位,所得函数图象对应的解析式为 ( )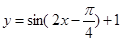
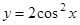
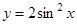
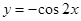
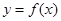 的图象向右平移
的图象向右平移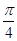 个单位,再向上平移1个单位后得到的函数对应的表达式为
个单位,再向上平移1个单位后得到的函数对应的表达式为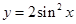 ,则函数
,则函数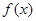 的表达式可以是
的表达式可以是