题目内容
已知集合P={x|y=log2（x-3）}，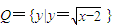
，则下列选项正确的是（ ）A．P=Q
B．P∩Q=∅
C．P
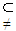QD．Q
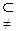P
【答案】分析：根据根式函数的值域，我们可以求出集合Q，根据对数函数的定义域，我们可以求出集合P，进而根据集合包含关系的判断方法得到两个集合之间的包含关系．
解答：解：∵y=
≥0，
∴集合
=[0，+∞）
若y=log2（x-3）的解析式有意义，
则x-3＞0，解得x＞3，
∴集合P=（4，+∞），
故P
Q．
故选C．
点评：本题考查的知识点是集合包含关系判断及应用，根式函数的图象和性质，对数函数的定义域，其中根据根式函数和对数函数的定义域及值域，求出集合P，Q是解答本题的关键．
解答：解：∵y=
≥0，∴集合
=[0，+∞）若y=log2（x-3）的解析式有意义，
则x-3＞0，解得x＞3，
∴集合P=（4，+∞），
故P
Q．故选C．
点评：本题考查的知识点是集合包含关系判断及应用，根式函数的图象和性质，对数函数的定义域，其中根据根式函数和对数函数的定义域及值域，求出集合P，Q是解答本题的关键．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知集合P={x|y=
，x，y∈R}，Q={y|x2+y2=4，x，y∈R}，则P∩Q=（ ）
| x+2 |
| A、{-2，1} | ||
B、{(-2，0)，(1，
| ||
| C、φ | ||
| D、Q |