Question

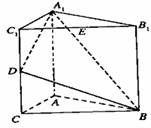
如图，直三棱柱A₁B₁C₁―ABC中C₁C=CB=CA=2，AC⊥CB. D、E分别为棱C₁C、B₁C₁的中点.

   （1）求点B的平面A₁C₁CA的距离；

   （2）求二面角B―A₁D―A的大小；

   （3）在线段AC上是否存在一点F，使得EF⊥平面A₁BD？若存在，确定其位置并证明结论；若不存在，说明理由.

Answer 1

解（1）∵A₁B₁C₁―ABC为直三棱柱

       ∴CC₁⊥底面ABC   ∴CC₁⊥BC

       ∵AC⊥CB  ∴BC⊥平面A₁C_­1CA

       ∴BC长度即为B点到平面A₁C₁CA的距离

       ∵BC=2  ∴点B到平面A₁C₁CA的距离为2

       （2）分别延长AC，A₁D交于G过C作CM⊥A₁G于M，连结BM

       ∵BC⊥平面ACC₁A₁ 

       ∴CM为BM在平面A₁C₁CA的内射影

       ∴BM⊥A₁G  ∴∠CMB为二面角B―A₁­D―A的平面角

       在平面A₁C₁CA中，C₁C=CA=2，D为C₁C的中点

       ∴CG=2，DC=1在直角三角形CDG中，

      

       即二面角B―A₁D―A的大小为

（3）在线段AC上存在一点F，使得EF⊥平面A₁BD

其位置为AC中点，证明如下                  

∵A₁B₁C₁―ABC为直三棱柱  ∴B₁C₁//BC

∵由（1）BC⊥平面A₁C₁CA， ∴B₁C₁⊥平面A₁C₁CA

∵EF在平面A₁C₁CA内的射影为C₁F 

∵F为AC中点   ∴C₁F⊥A₁D

∴EF⊥A₁D

同理可证EF⊥BD    ∴EF⊥平面A₁BD  

∵E为定点，平面A₁BD为定平面

∴点F唯一