题目内容
已知x∈[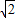 ,8],试求函数f(x)=log2
,8],试求函数f(x)=log2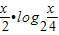 的最大值和最小值.
的最大值和最小值.
【答案】分析:由x∈[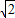 ,8],得log2x∈
,8],得log2x∈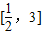 ,f(x)可化为关于log2x的二次函数,配方后可求得其最大值、最小值.
,f(x)可化为关于log2x的二次函数,配方后可求得其最大值、最小值.
解答:解:因为x∈[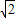 ,8],所以log2x∈
,8],所以log2x∈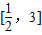 ,
,
f(x)=log2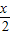 •
•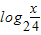 =(log2x-1)(log2x-2)=
=(log2x-1)(log2x-2)=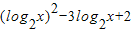 =
=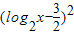 -
- ,
,
故当log2x=3时,f(x)max=2,
当log2x= 时,
时,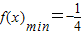 .
.
点评:本题考查复合函数的单调性、二次函数对数函数的性质,考查学生的运算能力.
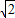 ,8],得log2x∈
,8],得log2x∈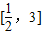 ,f(x)可化为关于log2x的二次函数,配方后可求得其最大值、最小值.
,f(x)可化为关于log2x的二次函数,配方后可求得其最大值、最小值.解答:解:因为x∈[
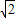 ,8],所以log2x∈
,8],所以log2x∈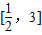 ,
,f(x)=log2
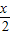 •
•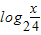 =(log2x-1)(log2x-2)=
=(log2x-1)(log2x-2)=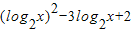 =
=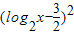 -
- ,
,故当log2x=3时,f(x)max=2,
当log2x=
 时,
时,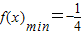 .
.点评:本题考查复合函数的单调性、二次函数对数函数的性质,考查学生的运算能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目


 x+1与y=
x+1与y= x+
x+ ,试利用“最小二乘法”判断哪条直线拟合程度更好.
,试利用“最小二乘法”判断哪条直线拟合程度更好.