题目内容
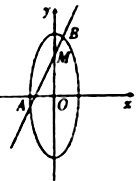
【题目】如图，已知焦点在
轴上的椭圆
的中心是原点
，离心率为
，以椭圆
的端州的两端点和两焦点所围成的四边形的周长为8，直线
：
与
轴交于点
，与椭圆
交于不同两点
，
．
（1）求椭圆
的标准方程；
（2）若
，求
的取值范围．
【答案】（1）
；（2）
.
【解析】
试题分析：（1）由焦点三角形的周长为
，可得
的值，运用离心率公式和
，
，
的关系，解方程可得
，
，进而得到椭圆方程；（2）由题意可得
，设
，
，运用向量共线的坐标表示和直线方程代入椭圆方程，运用韦达定理，可得
，代入
，再由不等式的性质，可得所求范围．
试题解析：（1）由已知可得以椭圆
的短轴的两端点和两焦点所围成的四边形的周长为
，
．
又
，∴
，
，
∴椭圆
的标准方程为．
（2）根据已知得，设，，
由
得
，
由已知得
，即
，
且
，
，
∵
，∴
，∴
，
代入上式可得
，
，
所以
，得，代入，
整理得
，∴
的取值范围是．
练习册系列答案
相关题目
【题目】为了研究某种微生物的生长规律，需要了解环境温度
（
）对该微生物的活性指标
的影响，某实验小组设计了一组实验，并得到如表的实验数据：
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
（Ⅰ）由表中数据判断关于
的关系较符合
还是
，并求关于的回归方程（
，
取整数）；
（Ⅱ）根据（Ⅰ）中的结果分析：若要求该种微生物的活性指标不能低于
，则环境温度应不得高于多少？
附：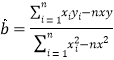
，