题目内容
(1)求过(-1,2),斜率为2的直线的参数方程.
(2)若直线3x+4y+m=0与圆
(θ为参数)没有公共点,求实数m的取值范围.
(2)若直线3x+4y+m=0与圆
|
分析:(1)可先写出普通方程,再化为参数方程.(2)先将圆的参数方程化为普通方程,再利用圆心到直线的距离大于半径即可求出m的取值范围.
解答:解:(1)∵直线l过(-1,2),斜率为2,∴直线l的普通方程为y-2=2(x+1),于是可得直线l的参数方程为
.
(2)将圆
(θ为参数)消去参数θ化为普通方程为(x-1)2+(y+2)2=1.
∵直线3x+4y+m=0与圆(x-1)2+(y+2)2=1没有公共点,∴圆心(1,-2)到直线的距离大于半径1,
∴
>1,解得m<0,或m>10.
∴实数m的取值范围为(-∞,0)∪(10,+∞).
|
(2)将圆
|
∵直线3x+4y+m=0与圆(x-1)2+(y+2)2=1没有公共点,∴圆心(1,-2)到直线的距离大于半径1,
∴
| |3-2×4+m| | ||
|
∴实数m的取值范围为(-∞,0)∪(10,+∞).
点评:本题考查了参数方程与普通方程的互化和直线与圆的位置关系,消去参数及把直线与圆的位置关系转化为圆心到直线的距离与半径的大小关系是解决问题的关键.

练习册系列答案
相关题目
 (θ为参数)没有公共点,求实数m的取值范围.
(θ为参数)没有公共点,求实数m的取值范围. .
.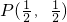 且被点P平分的弦所在直线的方程;
且被点P平分的弦所在直线的方程;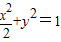 .
.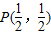 且被点P平分的弦所在直线的方程;
且被点P平分的弦所在直线的方程;