题目内容
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2,
(Ⅰ)求证:PD⊥BC;
(Ⅱ)求二面角B-PD-C的大小。
(Ⅰ)求证:PD⊥BC;
(Ⅱ)求二面角B-PD-C的大小。
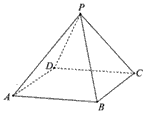
| (Ⅰ)证明:∵平面PCD⊥平面ABCD, 又∵平面PCD∩平面ABCD=CD,BC在平面ABCD内,BC⊥CD, ∴BC⊥平面PCD, ∴PD⊥BC。 |
|
| (II)解:取PD的中点E,连接CE、BE, ∵△PDC为正三角形, ∴CE⊥DP,由(Ⅰ)知BC⊥平面PCD, ∴CE是BE在平面PCD内的射影, ∴BE⊥PD, ∴∠CEB为二面角B-PD-C的平面角, 在△ABC中,∠BCE=90°,BC=2,  , , , ,∴二面角B-PD-C的大小为  。 。 |
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
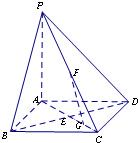 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.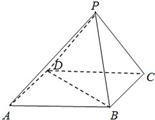 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.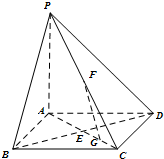 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.