��Ŀ����
����Ŀ���������������ڵ�����һ�����ι۹���Ŀ,��Ʒ������£���ͼ��ʾ��ԲO��Բ�κ��ı߽�,���߶�AB,BC,CD,DA��һ���۾�����,����A,B,C,D�ǹ۾����ȵ��ĸ�������Ҷ���ԲO�ϣ���֪��BC=12����,AB=8����,�ں���P���ͺ���D������һ���۾�ͤ,�����ǹ���ֱ��AC�Գ�,�ں��潨һ���۾���APC.�۾�ͤ�Ĵ�С���۾����ȡ��۾��ŵĿ��Ⱦ����Բ��ƣ���![]() ��
��
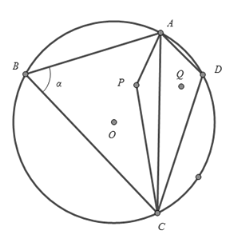
��1�����۾�����AD��4���ף�CD=AB�����ɹ۾�������Χ�ɵ��ı���ABCD�ڵĺ��������
��2����![]() ʱ��������������ADC�ڵĺ�����������ֵ��
ʱ��������������ADC�ڵĺ�����������ֵ��
��3����CD=8�����ҹ滮��ͤ��P��������ABC�����ڣ��������߽磩�����ж��ı���ABCP�ں�������Ƿ������ֵ�����У�������ֵ����д����ʱ![]() ��ֵ����û�У���˵�����ɣ�
��ֵ����û�У���˵�����ɣ�
���𰸡���1��![]() ƽ�����ף���2��
ƽ�����ף���2��![]() ƽ�����ף���3����
ƽ�����ף���3����![]() =
=![]() ʱ���ı���ABCP�ڵĺ������ȡ�����ֵ�� ���ֵΪ32ƽ������.
ʱ���ı���ABCP�ڵĺ������ȡ�����ֵ�� ���ֵΪ32ƽ������.
��������
��1���ֱ���![]() ��
��![]() ���������Ҷ��������
���������Ҷ��������![]() �������ɵ�
�������ɵ�![]() ��
��![]() ������
������![]() ���ɵý������2����
���ɵý������2����![]() �У��ɵ�
�У��ɵ�![]() ����
����![]() ��
��![]() ����
����![]() �У��������Ҷ����ɵ�
�У��������Ҷ����ɵ�![]() ���ɻ�������ʽ�ɵ�
���ɻ�������ʽ�ɵ�![]() ����
����![]() ���ɵý������3�������
���ɵý������3�������![]() �������
�������![]() �������ɵý��.
�������ɵý��.
�⣺��1�����ı���ABCD�ڽ���ԲO����![]() ABC+
ABC+![]() ADC=
ADC=![]()
��![]() ��
�У�![]()
��![]() ��
�У�![]()
���![]() ����
����![]()
��![]()
��ƽ�����ף�
���ı���ABCD�ڵĺ��������![]() ƽ������.
ƽ������.
��2����![]() =60
=60![]() ������
������![]() ��
�У�![]() =112
=112
��![]() ��
��![]() �� ��
�� ��![]() ��
�У�![]() =112
=112
��![]() =112
=112
��![]()
��![]() �����ҽ���x=yʱ��ȡ�Ⱥţ�
�����ҽ���x=yʱ��ȡ�Ⱥţ�
��![]()
��![]() ��ƽ�����ף�
��ƽ�����ף�
������������ADC�ڵĺ���������ֵ![]() ƽ�����ף�
ƽ�����ף�
��3���ߵ�P�͵�D����ֱ��AC�Գƣ�
��![]() APC=
APC=![]() ADC��PC=CD=8
ADC��PC=CD=8
�ɣ�1��֪![]() ABC+
ABC+![]() ADC=
ADC=![]() ����
����![]() ABC+
ABC+![]() APC=
APC=![]()
��![]() ABC=
ABC=![]() ����
����![]() APC=
APC=![]()
![]()
�ߵ�P��![]() ������
������
��![]() ����
����![]()
����![]() ��
�У�![]()
��![]() ��
�У�![]()
��![]()
���![]() ��
��![]() ����ȥ��
����ȥ��
![]()
![]()
��![]() �����ı���ABCP�ڵĺ�����������ֵ��
�����ı���ABCP�ڵĺ�����������ֵ��
�𣺵�![]() =
=![]() ʱ���ı���ABCP�ڵĺ������ȡ�����ֵ�����ֵΪ32ƽ������
ʱ���ı���ABCP�ڵĺ������ȡ�����ֵ�����ֵΪ32ƽ������