题目内容
已知x是函数f（x）=2x+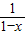
的一个零点．若x1∈（1，x），x2∈（x，+∞），则（ ）A．f（x1）＜0，f（x2）＜0
B．f（x1）＜0，f（x2）＞0
C．f（x1）＞0，f（x2）＜0
D．f（x1）＞0，f（x2）＞0
【答案】分析：因为x是函数f（x）=2x+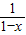
的一个零点 可得到f（x）=0，再由函数f（x）的单调性可得到答案．
解答：解：∵x是函数f（x）=2x+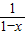
的一个零点∴f（x）=0
∵f（x）=2x+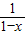
是单调递增函数，且x1∈（1，x），x2∈（x，+∞），
∴f（x1）＜f（x）=0＜f（x2）
故选B．
点评：本题考查了函数零点的概念和函数单调性的问题，属中档题．
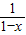的一个零点 可得到f（x）=0，再由函数f（x）的单调性可得到答案．解答：解：∵x是函数f（x）=2x+
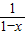的一个零点∴f（x）=0∵f（x）=2x+
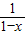是单调递增函数，且x1∈（1，x），x2∈（x，+∞），∴f（x1）＜f（x）=0＜f（x2）
故选B．
点评：本题考查了函数零点的概念和函数单调性的问题，属中档题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知函数f（x）、g（x），下列说法正确的是（ ）
| A、f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数 | B、f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数 | C、f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数 | D、f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数 |
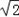是函数f（x）=
的极值点．
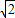是函数f（x）=
的极值点．
是函数f（x）=
的极值点．