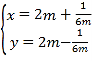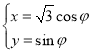题目内容
【题目】在四棱锥![]() 中,
中,![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,![]() 为矩形,
为矩形,![]() ,
,![]() .若四棱锥
.若四棱锥![]() 的顶点均在球
的顶点均在球![]() 的球面上,则球
的球面上,则球![]() 的表面积为_____.
的表面积为_____.
【答案】![]()
【解析】
做![]() 中点
中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,由已知条件可求出
,由已知条件可求出![]() ,运用余弦定理可求
,运用余弦定理可求![]() ,从而在平面
,从而在平面![]() 中建立坐标系,则
中建立坐标系,则![]() 以及
以及![]() 的外接圆圆心为
的外接圆圆心为![]() 和长方形
和长方形![]() 的外接圆圆心为
的外接圆圆心为![]() 在该平面坐标系的坐标可求,通过球心
在该平面坐标系的坐标可求,通过球心![]() 满足
满足![]() ,即可求出
,即可求出![]() 的坐标,从而可求球的半径,进而能求出球的表面积.
的坐标,从而可求球的半径,进而能求出球的表面积.
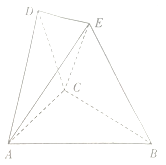
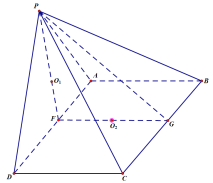
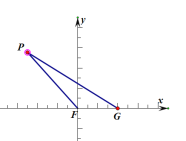
解:如图做![]() 中点
中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,由题意知
,由题意知
![]() ,则
,则![]()
设![]() 的外接圆圆心为
的外接圆圆心为![]() ,则
,则![]() 在直线
在直线![]() 上且
上且![]()
设长方形![]() 的外接圆圆心为
的外接圆圆心为![]() ,则
,则![]() 在
在![]() 上且
上且![]() .设外接球的球心为
.设外接球的球心为![]()
在![]() 中,由余弦定理可知
中,由余弦定理可知![]() ,
,![]() .
.
在平面![]() 中,以
中,以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,以过
轴,以过![]() 点垂直于
点垂直于![]() 轴的直
轴的直
线为![]() 轴,如图建立坐标系,由题意知,
轴,如图建立坐标系,由题意知,![]() 在平面
在平面![]() 中且
中且![]()
设![]() ,则
,则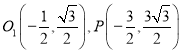 ,因为
,因为![]() ,所以
,所以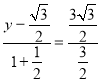
解得![]() .则
.则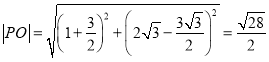
所以球的表面积为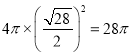 .
.
故答案为: ![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市对全市高二学生的期末数学测试成绩统计显示,全市10000名学生的数学成绩服从正态分布![]() .现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
.现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
注:表中试卷编![]() .
.
(1)写出表中试卷得分为144分的试卷编号(写出具体数据即可);
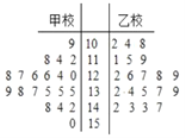
(2)该市又用系统抽样的方法从乙校中抽取了20份试卷,将甲乙两校这40份试卷的得分制作成如图所示的茎叶图,在这40份试卷中,从成绩在140分以上(含140分)的学生中任意抽取3人,这3人中数学成绩在全市排名前15名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]()
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关):
的统计数据如下表(已知该公司的年利润与年份代号线性相关):
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年(年份代号记为
的线性回归方程,并预测该公司2020年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由![]() 中线性回归方程计算出该年利润的估计值时,称该年为
中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将
级利润年.将![]() 中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这
中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: