题目内容
函数 的单调增区间为________.
的单调增区间为________.
(2,6)
分析:先求出函数的定义域为:(-2,6),再换元:令t= ,根据复合函数的单调性,t关于x的减区间就是函数
,根据复合函数的单调性,t关于x的减区间就是函数 的增区间,由此不难得到正确答案.
的增区间,由此不难得到正确答案.
解答:其中12+4x-x2>0,解之得-2<x<6
∴y= ,(t>0),可得y是关于t的减函数
,(t>0),可得y是关于t的减函数
∴当t= 为关于x的减函数时,函数
为关于x的减函数时,函数 为单调增函数
为单调增函数
∵t= 的被开方数对应开口向下的抛物线,在区间(2,6)上为减函数
的被开方数对应开口向下的抛物线,在区间(2,6)上为减函数
∴t= 的单调减区间为(2,6)
的单调减区间为(2,6)
综上所述,函数 的单调增区间为(2,6)
的单调增区间为(2,6)
故答案为:(2,6)
点评:本题以复合函数为例,求函数的单调区间,着重考查了函数的定义域、二次函数的单调性的反比例函数的单调性等知识,属于基础题.
分析:先求出函数的定义域为:(-2,6),再换元:令t=
 ,根据复合函数的单调性,t关于x的减区间就是函数
,根据复合函数的单调性,t关于x的减区间就是函数 的增区间,由此不难得到正确答案.
的增区间,由此不难得到正确答案.解答:其中12+4x-x2>0,解之得-2<x<6
∴y=
 ,(t>0),可得y是关于t的减函数
,(t>0),可得y是关于t的减函数∴当t=
 为关于x的减函数时,函数
为关于x的减函数时,函数 为单调增函数
为单调增函数∵t=
 的被开方数对应开口向下的抛物线,在区间(2,6)上为减函数
的被开方数对应开口向下的抛物线,在区间(2,6)上为减函数∴t=
 的单调减区间为(2,6)
的单调减区间为(2,6)综上所述,函数
 的单调增区间为(2,6)
的单调增区间为(2,6)故答案为:(2,6)
点评:本题以复合函数为例,求函数的单调区间,着重考查了函数的定义域、二次函数的单调性的反比例函数的单调性等知识,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
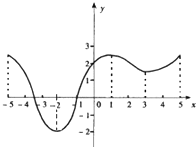 如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( )
如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( ) 的单调增区间为(0,+∞),则实数
的单调增区间为(0,+∞),则实数 的取值范围是________.
的取值范围是________. 的单调增区间为_________________。
的单调增区间为_________________。