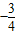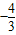题目内容
已知
，且α是第三象限的角，则
=（ ）A．
B．
C．
D．
【答案】分析：由sinα的值，以及α为第三象限角，利用同角三角函数间的基本关系求出cosα，所求式子利用两角和与差的正弦函数公式及特殊角的三角函数值化简，将各自的值代入计算即可求出值．
解答：解：∵sinα=-
，α是第三象限的角，
∴cosα=-
=-
，
则sin（α+
）=
sinα+
cosα=
×（-
-
）=-
．
故选D
点评：此题考查了两角和与差的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．
解答：解：∵sinα=-
，α是第三象限的角，∴cosα=-
=-，则sin（α+
）=sinα+cosα=×（--）=-．故选D
点评：此题考查了两角和与差的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
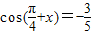，且x是第三象限角，则
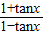的值为（ ）
