题目内容
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,求证:函数
,求证:函数![]() 的极大值小于1.
的极大值小于1.
【答案】(1)见解析;(2)![]() (3)见证明
(3)见证明
【解析】
(1)先对函数求导,分别讨论![]() 和
和![]() ,即可得出结果;
,即可得出结果;
(2)先将函数![]() 在
在![]() 时恒成立,转化为
时恒成立,转化为![]() 在
在![]() 上恒成立,再设
上恒成立,再设![]() ,
,![]() ,利用导数方法求出
,利用导数方法求出![]() 的最大值,即可得出结果;
的最大值,即可得出结果;
(3)先由题意得到![]() ,对
,对![]() 求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
解:(1)由于![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
(2)若![]() 在
在![]() 上恒成立,
上恒成立,
只需![]() ,
,![]() .
.
令![]() ,
,![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,所以
,所以
![]() ,
,![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
| 1 |
|
| + | 0 | - |
|
| 极大值 |
|
所以![]() ,所以
,所以![]() .
.
(3)由题知![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
所以存在唯一的![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
,
其中![]() ,所以函数
,所以函数![]() 有极大值.
有极大值.
函数![]() 的极大值是
的极大值是![]() ,由
,由![]() ,得
,得![]() ,
,
所以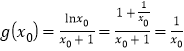 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 的极大值小于1.
的极大值小于1.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.