题目内容
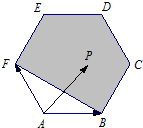 在正六边形ABCDEF中,AB=1,
在正六边形ABCDEF中,AB=1,| AP |
| AB |
| AF |
[1,4]
[1,4]
.分析:通过建立坐标系,写出点的坐标及直线方程,设动点P的坐标写出动点P的可行域;写出向量的坐标,据已知条件中的向量等式得到α,β与x,y的关系代入点P的可行域得α,β的可行域,利用线性规划求出α+β的取值范围.
解答: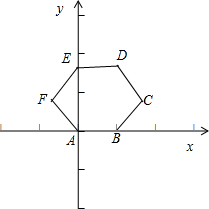 解:建立如图坐标系,∵AB=1,则A(0,0),B(1,0),C(
解:建立如图坐标系,∵AB=1,则A(0,0),B(1,0),C(
,
),D(1,
),E(0,
),F(-
,
).
则CD的方程:
x+ y-2
=0;BC的方程:
•x- y-
=0;EF 的方程:
x- y+
=0;BF的方程:x+
y-1=0.
设
=(α,β),
因P是五边形BCDEF内的动点,则可行域为
.
由
=(1,0),
=(-
,
),所以(α,β)=x(1,0)+y(-
,
).
得
,可得
,化简可得
,
由线性规划的知识解得1≤x+y≤4.
故答案为:[1,4].
 解:建立如图坐标系,∵AB=1,则A(0,0),B(1,0),C(
解:建立如图坐标系,∵AB=1,则A(0,0),B(1,0),C(| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
则CD的方程:
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
设
| AP |
因P是五边形BCDEF内的动点,则可行域为
|
由
| AB |
| AF |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
得
|
|
|
由线性规划的知识解得1≤x+y≤4.
故答案为:[1,4].
点评:本题考查通过建立直角坐标系将问题转化为线性规划问题,通过线性规划求出范围.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
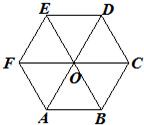 O是正六边形ABCDE的中心,且
O是正六边形ABCDE的中心,且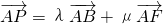 (λ,μ∈R)则λ+μ的取值范围
(λ,μ∈R)则λ+μ的取值范围 (λ,μ∈R)则λ+μ的取值范围( )
(λ,μ∈R)则λ+μ的取值范围( )