Question

（09年崇文区期末理）（14分）

 已知椭圆的中心在坐标原点，左顶点，离心率，为右焦点，过焦点的直线交椭圆于、两点（不同于点）．

（Ⅰ）求椭圆的方程；

（Ⅱ）当时，求直线PQ的方程；

（Ⅲ）判断能否成为等边三角形，并说明理由．

Answer 1

解析：（Ⅰ）设椭圆方程为 (a>b>0) ，

由已知

∴                 ------------------------------------2分

      ∴ 椭圆方程为．           --------------------------------------------4分

（Ⅱ）解法一

椭圆右焦点．

设直线方程为（∈R）．          ----------------------------5分

由    得．①          --------6分

显然，方程①的．

设，则有．     --7分

     ．

∵，

∴ ．

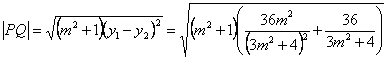
解得．

∴直线PQ 方程为，即或．    ----------9分

解法二： 椭圆右焦点．

当直线的斜率不存在时，，不合题意．

设直线方程为，            --------------------------------------5分

由  得．   ①     ----6分

显然，方程①的．

设，则．      --------7分

   

    =．

∵，

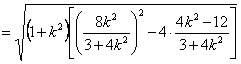
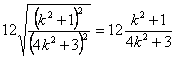∴，解得．

∴直线的方程为，即或．  --------9分

   （Ⅲ）不可能是等边三角形．   ---------------------------------------------------11分

     如果是等边三角形，必有，

      ∴，

∴，

∴，

∵，

∴，

∴，

     ∴，或（无解）．

     而当时，，不能构成等边三角形．

     ∴不可能是等边三角形．------------------------------------------------------------14分