Question

（2012•济宁一模）已知函数f(x)=x-lnx，g(x)=

lnx

x

．
（I）求函数f（x）的单调区间；
（II）求证：对任意的m，n∈（0，e]，都有f（m）-g（n）＞

1

2

．
（注：e≈2.71828…是自然对数的底数．）

Answer 1

分析：（I）由y=x-lnx，知x＞0，y′=1-

1

x

，由y′=1-

1

x

=0，得x=1．由此能求出函数的单调区间．
（II）由（1）知函数y=x-lnx的增区间是[1，+∞），减区间是（0，1]．由此能求出函数f（x）的最小值．由g（x）=

lnx

x

，知g′（x）=

1-lnx

x2

，由此能求出函数g（x）=

lnx

x

的单调区间，由此能求出函g（x）数的最大值，最后根据f（x）的最小值-g（x）的最大值＞

1

2

，即可得到结果．

解答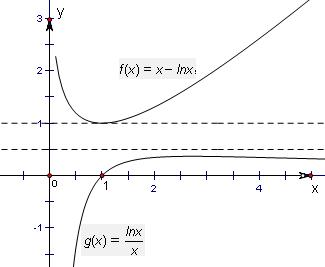：解：（I）∵y=x-lnx，
∴x＞0，y′=1-

1

x

，
由y′=1-

1

x

=0，得x=1．
当0＜x＜1时，y′＜0；当x＞1时，y′＞0，
∴函数y=x-lnx的增区间是[1，+∞），减区间是（0，1]．
（II）由（I）知y′=1-

1

x

，
由y′=1-

1

x

=0，得x=1．
函数y=x-lnx的增区间是[1，+∞），减区间是（0，1]．
∴当x=1时，函数取最小值y_min=1-ln1=1．
又∵g（x）=

lnx

x

，x＞0，故其定义域为（0，+∞）
∴g′（x）=

1-lnx

x2

，
令g′（x）＞0，得0＜x＜e
令g′（x）＜0，得x＞e
故函数g（x）=

lnx

x

的单调递增区间为（0，e），单调递减区间为（e，+∞）．
∴当x=e时，函数取最小值y_max=

1

e

．如图．
从图象中可以看出，在区间（0，e]上，f（x）的最小值减去g（x）的最大值大于

1

2

，
即对任意的m，n∈（0，e]，都有f（m）-g（n）＞

1

2

．

点评：本题考查函数的单调区间和函数的最值的求法，是基础题．解题时要认真审题，仔细解答．