题目内容
若函数f(x)=x2+ax-1,(a∈R)在区间[-1,1]上的最小值为-14,求a的值.
解:二次函数图象的对称轴方程为 ;
;
(1)当 ,即a≥2时;y最小=f(-1)=-a,
,即a≥2时;y最小=f(-1)=-a,
依题意知a=14.(5分)
(2)当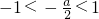 ,即-2<a<2时;
,即-2<a<2时; ,
,
依题意知 ,解得
,解得 (舍去).(7分)
(舍去).(7分)
(3)当 ,即a≤-2时;y最小=f(1)=a,
,即a≤-2时;y最小=f(1)=a,
依题意知a=-14.
综上所述:a=±14.(12分)
分析:由已知中函数f(x)=x2+ax-1,(a∈R)在区间[-1,1]上的最小值为-14,根据二次函数在定区间上最值的求法,分别分析区间在函数对称轴左侧、区间在函数对称轴右侧、区间在函数对称轴两侧三种情况下a的取值,综合后可得答案.
点评:本题考查的知识点是二次函数的性质,其中熟练掌握二次函数在定区间上最值的求法,是解答本题的关键.
 ;
;(1)当
 ,即a≥2时;y最小=f(-1)=-a,
,即a≥2时;y最小=f(-1)=-a,依题意知a=14.(5分)
(2)当
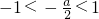 ,即-2<a<2时;
,即-2<a<2时; ,
,依题意知
 ,解得
,解得 (舍去).(7分)
(舍去).(7分)(3)当
 ,即a≤-2时;y最小=f(1)=a,
,即a≤-2时;y最小=f(1)=a,依题意知a=-14.
综上所述:a=±14.(12分)
分析:由已知中函数f(x)=x2+ax-1,(a∈R)在区间[-1,1]上的最小值为-14,根据二次函数在定区间上最值的求法,分别分析区间在函数对称轴左侧、区间在函数对称轴右侧、区间在函数对称轴两侧三种情况下a的取值,综合后可得答案.
点评:本题考查的知识点是二次函数的性质,其中熟练掌握二次函数在定区间上最值的求法,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目