题目内容
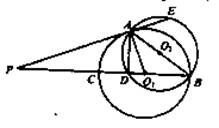
如图，圆O1与圆O2相交于A、B两点，AB是圆O2的直径，过A点作圆O1的切线交圆O2于点E，并与BO1的延长线交于点P，PB分别与圆O1、圆O2交于C，D两点.
求证：(Ⅰ)PA·PD=PE·PC；
(Ⅱ)AD=AE.
【答案】
（Ⅰ）见解析（Ⅱ）见解析
【解析】(I)本小题根据切割线定理，及割线定理可知
和
, 然后两式结合可得
(II)利用分析法要证：AD=AE
然后根据题目条件进行推证即可证出结论.
（Ⅰ）
分别是⊙
的割线∴
①（2分）
又
分别是⊙
的切线和割线∴ ② （4分）
由①，②得
（5分）
（Ⅱ）连结
、
设
与
相交于点
∵
是⊙的直径∴
∴是⊙的切线. （6分）
由（Ⅰ）知
，∴∥∴⊥, 
（8分）
又∵是⊙的切线，∴ 
又，∴
∴
练习册系列答案
阅读快车系列答案
相关题目
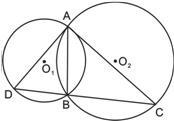圆O1与圆O2相交于A、B，过A作圆O1的切线交圆O2于C，连CB并延长交圆O1于D，连AD，AB=2，BD=3，BC=5，求AD的长．
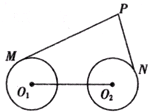如图，圆O1与圆O2的半径都是1，O1O2=4，过动点P分别作圆O1．圆O2的切线PM、PN（M．N分别为切点），使得PM=
A．选修4-1：几何证明选讲