题目内容
如图,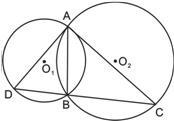 圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,求AD的长.
圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,求AD的长.
分析:首先根据题中圆的切线条件再依据切割线定理求得AC2的值,再根据勾股定理即可求得AD的长.
解答:解:∵AC是圆O2的切线,
∴∠CAB=∠D,
又∵∠C=∠C,
∴△ACD∽△BCA,
∴AC2=BC•CD,AB=2,BD=3,BC=5,
∴AC2=40,
∴AD=
=2
.
故AD的长是2
.
∴∠CAB=∠D,
又∵∠C=∠C,
∴△ACD∽△BCA,
∴AC2=BC•CD,AB=2,BD=3,BC=5,
∴AC2=40,
∴AD=
| 64-40 |
| 6 |
故AD的长是2
| 6 |
点评:此题综合运用了切割线定理、切线的性质定理以及勾股定理.本题主要考查与圆有关的比例线段、圆中的切割线定理,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
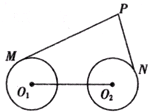 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM=
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM= A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲