题目内容
函数f(x)= +lnx(a≠0),
+lnx(a≠0),
(1)求函数y=f(x)的递增区间;
(2)当a=1时,求函数y=f(x)在[ ,4]上的最大值和最小值;
,4]上的最大值和最小值;
(3)求证: 。
。
 +lnx(a≠0),
+lnx(a≠0),(1)求函数y=f(x)的递增区间;
(2)当a=1时,求函数y=f(x)在[
 ,4]上的最大值和最小值;
,4]上的最大值和最小值;(3)求证:
 。
。 (1)解: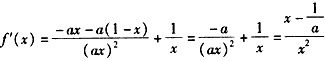 ,
,
①若a<0,f′(x)>0对一切x>0恒成立,∴f(x)的增区间为(0,+∞);
②若a>0,则当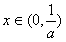 时,f′(x)<0,函数f(x)单调递减;
时,f′(x)<0,函数f(x)单调递减;
当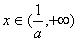 时,f′(x)>0,函数f(x)单调递增;
时,f′(x)>0,函数f(x)单调递增;
故当a<0时,f(x)的增区间为(0,+∞),当a>0时,f(x)的增区间为 ;
;
(2)解:当a=1时,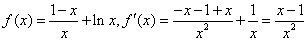 ,
,
当x变化时,f(x),f′(x)的变化情况如下表:
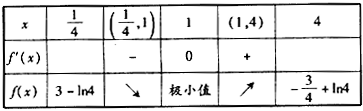
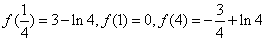 ,
,
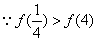 ,
,
∴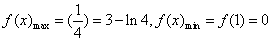 。
。
(3)证明:当a=1时,由(2)知f(x)≥f(1)=0,
∴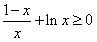 ,即
,即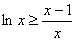 (当且仅当x=1时取等号),
(当且仅当x=1时取等号),
①令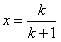 ,则有
,则有 (此时等号不成立),
(此时等号不成立),
即有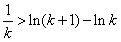 ,
,
∴当k=n+1时,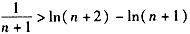 ,
,
当k=n+2时,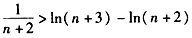 ,
,
……
当k=3n时,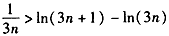 ,
,
累加可得: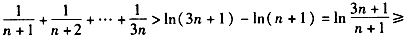
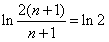 。
。
②同理令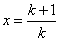 ,则有
,则有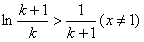 (此时等号不成立),
(此时等号不成立),
即有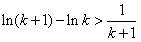 ,
,
∴当k=n时,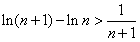 ,
,
当k=n+1时,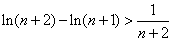 ,
,
当k=3n-1时,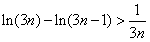 ,
,
累加可得: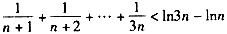 ,
,
即: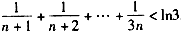 ,
,
故: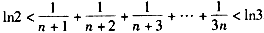 。
。
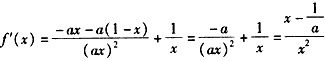 ,
,①若a<0,f′(x)>0对一切x>0恒成立,∴f(x)的增区间为(0,+∞);
②若a>0,则当
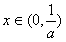 时,f′(x)<0,函数f(x)单调递减;
时,f′(x)<0,函数f(x)单调递减;当
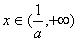 时,f′(x)>0,函数f(x)单调递增;
时,f′(x)>0,函数f(x)单调递增;故当a<0时,f(x)的增区间为(0,+∞),当a>0时,f(x)的增区间为
 ;
;(2)解:当a=1时,
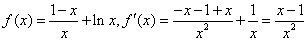 ,
,当x变化时,f(x),f′(x)的变化情况如下表:

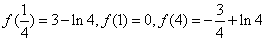 ,
,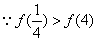 ,
,∴
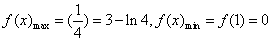 。
。 (3)证明:当a=1时,由(2)知f(x)≥f(1)=0,
∴
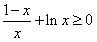 ,即
,即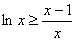 (当且仅当x=1时取等号),
(当且仅当x=1时取等号), ①令
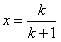 ,则有
,则有 (此时等号不成立),
(此时等号不成立),即有
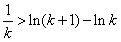 ,
,∴当k=n+1时,
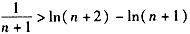 ,
,当k=n+2时,
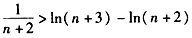 ,
,……
当k=3n时,
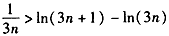 ,
,累加可得:
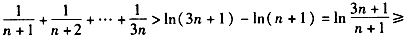
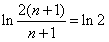 。
。②同理令
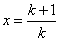 ,则有
,则有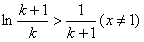 (此时等号不成立),
(此时等号不成立),即有
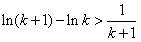 ,
,∴当k=n时,
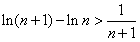 ,
,当k=n+1时,
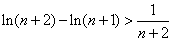 ,
,当k=3n-1时,
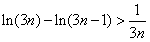 ,
,累加可得:
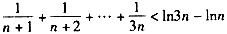 ,
,即:
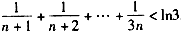 ,
,故:
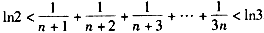 。
。 
练习册系列答案
相关题目