题目内容
已知A、B、C是△ABC的内角,向量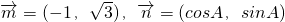 ,且
,且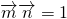 .
.
(1)求角A;
(2)若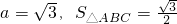 ,求b和c的值.
,求b和c的值.
解:(1)由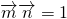 ,得到-cosA+
,得到-cosA+ sinA=1,
sinA=1,
即 sinA-cosA=1,化简得sin(A-
sinA-cosA=1,化简得sin(A- )=
)= ,
,
∵0<A<π,∴- <A-
<A- <
< ,
,
∴A- =
= ,即A=
,即A= ;
;
(2)由cosA= ,可知
,可知 =
= ,即(b+c)2-a2=3bc①,
,即(b+c)2-a2=3bc①,
又S△ABC= bcsinA=
bcsinA= ,得bc=2,又a=
,得bc=2,又a= ,
,
代入①得:b+c=3,
联立得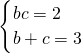 ,解得:
,解得: 或
或 .
.
分析:(1)根据平面向量的数量积运算法则,化简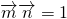 ,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;
,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;
(2)根据(1)求出的A的度数,计算得到cosA的值,然后利用余弦定理表示出cosA,化简得到一个关系式,记作①,然后再根据三角形的面积公式,由sinA的值求出bc的值,把bc和a的值代入①即可列出b与c的二元一次方程组,求出方程组的解即可得到b与c的值.
点评:此题考查了三角函数的恒等变换,余弦定理及三角形的面积公式.要求学生掌握两角和与差得正弦函数公式,牢记特殊角的三角函数值.
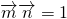 ,得到-cosA+
,得到-cosA+ sinA=1,
sinA=1,即
 sinA-cosA=1,化简得sin(A-
sinA-cosA=1,化简得sin(A- )=
)= ,
,∵0<A<π,∴-
 <A-
<A- <
< ,
,∴A-
 =
= ,即A=
,即A= ;
;(2)由cosA=
 ,可知
,可知 =
= ,即(b+c)2-a2=3bc①,
,即(b+c)2-a2=3bc①,又S△ABC=
 bcsinA=
bcsinA= ,得bc=2,又a=
,得bc=2,又a= ,
,代入①得:b+c=3,
联立得
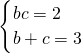 ,解得:
,解得: 或
或 .
.分析:(1)根据平面向量的数量积运算法则,化简
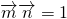 ,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;
,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;(2)根据(1)求出的A的度数,计算得到cosA的值,然后利用余弦定理表示出cosA,化简得到一个关系式,记作①,然后再根据三角形的面积公式,由sinA的值求出bc的值,把bc和a的值代入①即可列出b与c的二元一次方程组,求出方程组的解即可得到b与c的值.
点评:此题考查了三角函数的恒等变换,余弦定理及三角形的面积公式.要求学生掌握两角和与差得正弦函数公式,牢记特殊角的三角函数值.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;
β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;