题目内容

设A、B为椭圆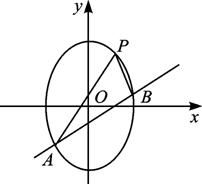=1上两动点，P（1，）为定点，若直线PA与PB的倾斜角互补（如图），求证：直线AB的斜率为定值.

证明：设直线PA的斜率为k，则直线PB的斜率为-k.将直线PA的方程y=k(x-1)+代入椭圆方程，得3x2+［k(x-1)+］2=6,

即(k2+3)x2-(2k2-2k)x+k2-2k-3=0.

显然P点在椭圆上，设A(x1,y1)，则x1和1是该方程的两根，由韦达定理，得x1=x1·1=

设B(x2,y2),同理可得

x2=.

∴kAB=

=

=

=

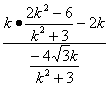
=，所以kAB为定值.

练习册系列答案
相关题目
已知点P (-1，  
3
2
)是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1、F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
（1）求椭圆E的方程；
（2）设A、B是椭圆E上两个动点，是否存在λ，满足
PA
+
PB
=λ
PO
（0＜λ＜4，且λ≠2），且M（2，1）到AB的距离为
5
？若存在，求λ值；若不存在，说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为2
3
，右焦点F与抛物线y2=4x的焦点重合，O为坐标原点．
（1）求椭圆C的方程；
（2）设A、B是椭圆C上的不同两点，点D（-4，0），且满足
DA
=λ
DB
，若λ∈[
3
8
，
1
2
]，求直线AB的斜率的取值范围．
（2012•泰州二模）已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点为F1（2，0），离心率为e．
（1）若e=
2
2
，求椭圆的方程；
（2）设A，B为椭圆上关于原点对称的两点，AF1的中点为M，BF1的中点为N，若原点O在以线段MN为直径的圆上．
①证明点A在定圆上；
②设直线AB的斜率为k，若k≥
3
，求e的取值范围．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的焦距为4，设右焦点为F1，离心率为e．
（1）若e=
2
2
，求椭圆的方程；
（2）设A、B为椭圆上关于原点对称的两点，AF1的中点为M，BF1的中点为N，若原点O在以线段MN为直径的圆上．
①证明点A在定圆上；
②设直线AB的斜率为k，若k≥
3
，求e的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网