题目内容

求以曲线x2+y2=25与y=x2-13的交点为顶点的多边形的面积.

解析：求多边形的面积，其关键是分析清楚该多边形的形状，如果是特殊多边形，可直接利用面积公式，如果是一般的多边形，则可将图形分割成三角形、特殊四边形等，所以要解方程求交点判断多边形的形状.

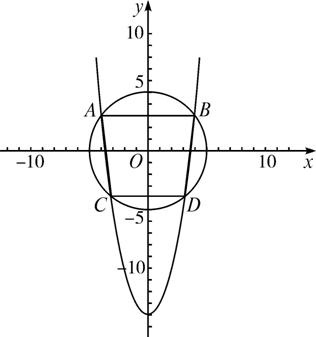
如图所示，解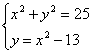得

或或或

可知该多边形ABCD是等腰梯形，且AB=8，CD=6，h=7.

所以S四边形ABCD= (AB+CD)h= (8+6)×7=49.

点评：作图象时注意利用圆和抛物线的对称性，在练习时，也可只画出四个交点，而忽略去圆和抛物线，显得实用快捷.

练习册系列答案
相关题目
（1）选修4-2：矩阵与变换
若矩阵A有特征值λ1=2，λ2=-1，它们所对应的特征向量分别为e1=
1
0
和e2=
0
1
．
（I）求矩阵A；
（II）求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程．
（2）选修4-4：坐标系与参数方程
已知曲线C1的参数方程为
x=2sinθ
y=cosθ
(θ为参数），C2的参数方程为
x=2t
y=t+1
(t为参数）
（I）若将曲线C1与C2上所有点的横坐标都缩短为原来的一半（纵坐标不变），分别得到曲线C′1和C′2，求出曲线C′1和C′2的普通方程；
（II）以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，求过极点且与C′2垂直的直线的极坐标方程．
（3）选修4-5：不等式选讲
设函数f（x）=|2x-1|+|2x-3|，x∈R，
（I）求关于x的不等式f（x）≤5的解集；
（II）若g(x)=
1
f(x)+m
的定义域为R，求实数m的取值范围．
求以曲线x2+y2=25与y=x2-13的交点为顶点的多边形的面积.

（1）选修4-2：矩阵与变换
若矩阵A有特征值λ1=2，λ2=-1，它们所对应的特征向量分别为e1=
1
0
和e2=
0
1
．
（I）求矩阵A；
（II）求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程．
（2）选修4-4：坐标系与参数方程
已知曲线C1的参数方程为
x=2sinθ
y=cosθ
(θ为参数），C2的参数方程为
x=2t
y=t+1
(t为参数）
（I）若将曲线C1与C2上所有点的横坐标都缩短为原来的一半（纵坐标不变），分别得到曲线C′1和C′2，求出曲线C′1和C′2的普通方程；
（II）以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，求过极点且与C′2垂直的直线的极坐标方程．
（3）选修4-5：不等式选讲
设函数f（x）=|2x-1|+|2x-3|，x∈R，
（I）求关于x的不等式f（x）≤5的解集；
（II）若g(x)=
1
f(x)+m
的定义域为R，求实数m的取值范围．
（1）选修4-2：矩阵与变换
若矩阵A有特征值λ1=2，λ2=-1，它们所对应的特征向量分别为．
（I）求矩阵A；
（II）求曲线x2+y2=1在矩阵A的变换下得到的新曲线方程．
（2）选修4-4：坐标系与参数方程
已知曲线C1的参数方程为为参数），C2的参数方程为为参数）
（I）若将曲线C1与C2上所有点的横坐标都缩短为原来的一半（纵坐标不变），分别得到曲线C′1和C′2，求出曲线C′1和C′2的普通方程；
（II）以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，求过极点且与C′2垂直的直线的极坐标方程．
（3）选修4-5：不等式选讲
设函数f（x）=|2x-1|+|2x-3|，x∈R，
（I）求关于x的不等式f（x）≤5的解集；
（II）若的定义域为R，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网