题目内容

定义在R上的偶函数y=f（x）在[0，+∞）上单调递减，函数f（x）的一个零点为
12
，则不等式f（log4x）＜0的解集是
 
．
分析：先根据条件，确定一个函数画出其图象，将log4x看作整体，利用所画图象求出其范围，再解关于x的不等式．
解答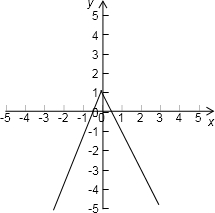：精英家教网解：根据条件：可画图：
如图所示：
log
x
4
＞
1
2
或
log
x
4
＜-
1
2

解得：x∈（0，
1
2
）∪（2，+∞）
故答案为：（0，
1
2
）∪（2，+∞）
点评：本题主要考查了函数的单调性奇偶性以及数形结合的解题方法．
练习册系列答案
相关题目
17、定义在R上的偶函数y=f（x）满足：
①对任意x∈R都有f（x+2）=f（x）+f（1）成立；
②f（0）=-1；
③当x∈（-1，0）时，都有f′（x）＜0．
若方程f（x）=0在区间[a，3]上恰有3个不同实根，则实数a的取值范围是
（-3，-1]
．
定义在R上的偶函数y=f（x）满足：①对x∈R都有f（x+6）=f（x）+f（3）；②当x1，x2∈[0，3]且x1≠x2时，都有
f(x1)-f(x2)x1-x2
＞0，若方程f（x）=0在区间[a，8-a]上恰有3个不同实根，实数a的取值范围是
（-7，-3）
（-7，-3）
．
定义在R上的偶函数y=f（x）在（-∞，0]上递增，函数f（x）的一个零点为-
1
2
，求满足f（log
1
9
x）≥0的x的取值集合．
定义在R上的偶函数y=f（x）满足f（x+2）=f（x），且当x∈（0，1]时单调递增，则（　　）
定义在R上的偶函数y=f （x）满足f （ x+2 ）=-f （x）对所有实数x都成立，且在[-2，0]上单调递增，a=f（
3
2
），b=f（
7
2
），c=f（log 
1
2
8），则a，b，c的由大到小顺序是（用“＞”连 结）
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网